
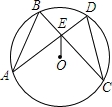
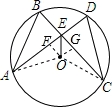
如图,在⊙O中,弦AD、BC相交于点E,连结OE,已知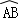 =
=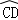 .
.
(1)求证:BE=DE;
(2)如果⊙O的半径为5,AD⊥CB,DE=1,求AE的长.
【考点】圆心角、弧、弦的关系;全等三角形的判定与性质.
【分析】(1)根据圆心角、弧、弦的关系得到AB=CD,推出△ABE≌△CDE,根据全等三角形的性质得到结论;
(2)过O作OF⊥AD与F,OG⊥BC于G,连接OA,OC,根据垂径定理得到AF=FD,BG=OG,由于AD=BC,于是得到AF=CG,推出Rt△AOF≌Rt△OCG,根据全等三角形的性质得到OF=OG,证得四边形OFEG是正方形,于是得到OF=EF,设OF=EF=x,则AF=FD=x+1,根据勾股定理即可得到结论.
【解答】解:(1)∵ =
=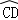 ,
,
∴AB=CD,
在△ABE与△CDE中,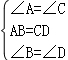 ,
,
∴△ABE≌△CDE,
∴BE=DE;
 (2)过O作OF⊥AD与F,OG⊥BC于G,连接OA,OC,
(2)过O作OF⊥AD与F,OG⊥BC于G,连接OA,OC,
根据垂径定理得:AF=FD,BG=OG,
∵AD=BC,
∴AF=OG,
在Rt△AOF与Rt△OCG中,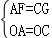 ,
,
∴Rt△AOF≌Rt△OCG,
∴OF=OG,
∵AD⊥CB,
∴四边形OFEG是正方形,
∴OF=EF,
设OF=EF=x,
则AF=FD=x+1,
∴OF2+AF2=OA2,
即:x2+(x+1)2=52,
解得:x=3,x=﹣4(舍去),
∴AF=4,
∴AE=7.
【点评】本题考查了全等三角形的判定和性质,圆心角、弧、弦的关系,勾股定理,熟练则全等三角形的判定和性质是解题的关键.


 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案 新思维寒假作业系列答案
新思维寒假作业系列答案科目:初中数学 来源: 题型:
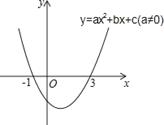
二次函数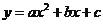 (
( )的图象如图所示,下列说法:①
)的图象如图所示,下列说法:① ,②当
,②当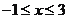 时,
时,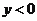 ,③若(
,③若(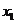 ,
,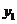 )、(
)、(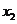 ,
,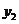 )在函数图象上,当
)在函数图象上,当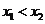 时,
时,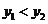 ,④
,④ ,其中正确的是( )
,其中正确的是( )
A.①②④ B.①④ C.①②③ D.③④
查看答案和解析>>
科目:初中数学 来源: 题型:
作图题,如图(4),已知:△ABC,读句作图,保留作图痕迹不写作法
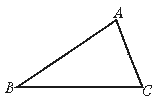
图(4)
(1)作∠B的平分线BD交AC于D.
(2)作高AE,E为垂足.
(3)作边AB的垂直平分线交AB于F.
(4)作∠AEM=∠ABC.
查看答案和解析>>
科目:初中数学 来源: 题型:
二次函数y=ax2+bx+c的图象如图,点C在y轴的正半轴上,且OA=OC,则( )

A.ac+1=b B.ab+1=c C.bc+1=a D.以上都不是
查看答案和解析>>
科目:初中数学 来源: 题型:
小米将两块相同的三角板摆成如图1的形状,三角板的斜边长为10cm,较小锐角为30°,点B、C、F、D在同一条直线上,且点C与点F重合,小米在对这两块三角板进行如下操作时遇到了如下问题,请你帮助他解决.
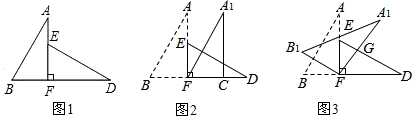
(1)将图1中的△ABC沿BD向右平移到图2的位置,使点B与点C重合,求出平移的距离;
(2)将图1中的△ABC绕点C顺时针方向旋转30°到图3的位置,A、C交DE于点G,求出线段GC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
三角形两边的长分别是8和6,第三边的长是方程x2﹣12x+20=0的一个实数根,则此三角形的周长是( )
A.24 B.24或16 C.16 D.22
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com