
【题目】如图1,在矩形ABCD中,点P是BC边上一点,连接AP交对角线BD于点E,![]() .作线段AP的中垂线MN分别交线段DC,DB,AP,AB于点M,G,F,N.
.作线段AP的中垂线MN分别交线段DC,DB,AP,AB于点M,G,F,N.
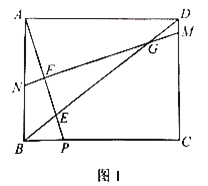
(1)求证:![]() ;
;
(2)若![]() ,求
,求![]() .
.
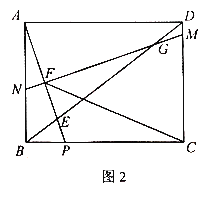
(3)如图2,在(2)的条件下,连接CF,求![]() 的值.
的值.
【答案】(1)见解析;(2)![]() ;(3)
;(3)![]()
【解析】
(1)由等角对等边可得![]() ,再由对顶角相等推出
,再由对顶角相等推出![]() ,然后利用等角的余角相等即可得证;
,然后利用等角的余角相等即可得证;
(2)在![]() 中,利用勾股定理可求出BD=10,然后由等角对等边得到
中,利用勾股定理可求出BD=10,然后由等角对等边得到![]() ,进而求出BP=2,再利用
,进而求出BP=2,再利用![]() 推出
推出![]() ,由垂直平分线推出
,由垂直平分线推出![]() ,即可得到
,即可得到![]() 的值;
的值;
(3)连接CG,先由勾股定理求出![]() ,由(2)的条件可推出BE=DG,再证明△ABE≌△CDG,从而求出
,由(2)的条件可推出BE=DG,再证明△ABE≌△CDG,从而求出![]() ,并推出
,并推出![]() ,最后在
,最后在![]() 中,即可求出
中,即可求出![]() 的值.
的值.
(1)证明:![]() ,
,
![]()
![]()
![]()
∵MN⊥AP
∴∠GFE=90°
∴∠BGN+∠GEF=90°
又![]()
![]()
![]()
(2)在矩形ABCD中,![]()
∴在![]() 中,
中,![]()
![]()
又∵在矩形ABCD中,![]()
![]()
![]()
![]()
![]()
![]()
![]()
∴![]()
![]()
![]()
∵MN垂直平分AP
![]()
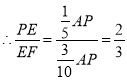
(3)如图,连接CG,

在![]() 中,
中,![]()
![]()
![]()
在![]() 中,
中,![]()
![]()
![]()
![]()
又∵在矩形ABCD中,![]()
![]()
在△ABE和△CDG中,
∵AB=DC,∠ABE=∠CDG,BE=DG
![]()
![]()
![]()
![]()
![]()
∴在![]() 中,
中,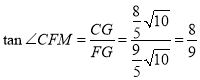


 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:初中数学 来源: 题型:
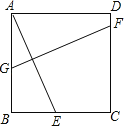
【题目】如图所示,正方形ABCD中,E为BC边上一点,连接AE,作AE的垂直平分线交AB于G,交CD于F,若BG=2BE,则DF:CF的长为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
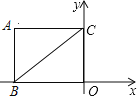
【题目】如图,平面直角坐标系中,矩形ABOC的边BO,CO分别在x轴,y轴上,A点的坐标为(﹣8,6),点P在矩形ABOC的内部,点E在BO边上,满足△PBE∽△CBO,当△APC是等腰三角形时,P点坐标为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() .
.
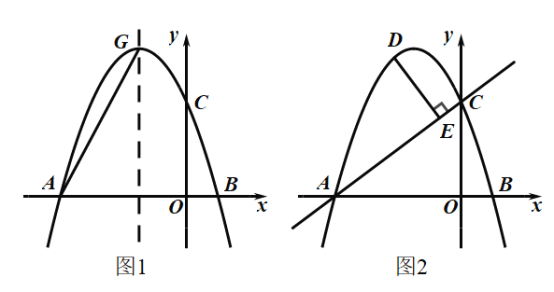
(1)求抛物线的解析式;
(2)如图1,抛物线的对称轴交抛物线于点![]() ,在
,在![]() 轴上是否存在点
轴上是否存在点![]() ,使得
,使得![]() 的周长最小?若存在,求出点
的周长最小?若存在,求出点![]() 坐标;若不存在,请说明理由;
坐标;若不存在,请说明理由;
(3)如图2,点![]() 为直线
为直线![]() 上方抛物线上的动点,
上方抛物线上的动点,![]() 于点
于点![]() ,求线段
,求线段![]() 的最大值.
的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着高铁的建设,春运期间动车组发送旅客量越来越大,相关部门为了进一步了解春运期间动车组发送旅客量的变化情况,针对2014年至2018年春运期间的铁路发送旅客量情况进行了调查,过程如下.
(Ⅰ)收集、整理数据
请将表格补充完整:
年份 | 2014 | 2015 | 2016 | 2017 | 2018 |
动车组发送旅客量a亿人次 | 0.87 | 1.14 | 1.46 | 1.80 | 2.17 |
铁路发送旅客总量b亿人次 | 2.52 | 2.76 | 3.07 | 3.42 | 3.82 |
动车组发送旅客量占比 | 34.5% | 41.3% | 47.6% | 52.6% |
(Ⅱ)描述数据
为了更直观地显示动车组发送旅客量占比的变化趋势,需要用 (填“折线图”或“扇形图”)进行描述;
(Ⅲ)分析数据、做出推测
预估2019年春运期间动车组发送旅客量占比约为 ,你的预估理由是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=BC,以AB为直径的⊙O与AC交于点D,过D作DF⊥BC, 交AB的延长线于E,垂足为F.
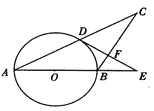
(1)求证:直线DE是⊙O的切线;
(2)当AB=5,AC=8时,求cosE的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
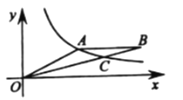
【题目】如图,![]() 是反比例函数
是反比例函数![]() 在第一象限图像上一点,连接
在第一象限图像上一点,连接![]() ,过
,过![]() 作
作![]() 轴,截取
轴,截取![]() (
(![]() 在
在![]() 右侧),连接
右侧),连接![]() ,交反比例函数
,交反比例函数![]() 的图像于点
的图像于点![]() .
.
(1)求反比例函数![]() 的表达式;
的表达式;
(2)求点![]() 的坐标及
的坐标及![]() 所在直线解析式;
所在直线解析式;
(3)求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,已知抛物线
中,已知抛物线![]() 经过点
经过点![]() ,对称轴是直线
,对称轴是直线![]() ,顶点为点
,顶点为点![]() ,抛物线与
,抛物线与![]() 轴交于点
轴交于点![]() .
.
(1)求抛物线的表达式和点![]() 的坐标;
的坐标;
(2)将上述抛物线向下平移![]() 个单位,平移后的抛物线与
个单位,平移后的抛物线与![]() 轴正半轴交于点
轴正半轴交于点![]() ,求
,求![]() 的面积;
的面积;
(3)如果点![]() 在原抛物线上,且在对称轴的右侧,联结
在原抛物线上,且在对称轴的右侧,联结![]() 交线段
交线段![]() 于点
于点![]() ,
,![]() ,求点
,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
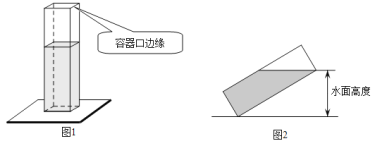
【题目】如图1,长、宽均为3,高为8的长方体容器,放置在水平桌面上,里面盛有水,水面高为6,绕底面一棱长进行旋转倾斜后,水面恰好触到容器口边缘,图2是此时的示意图,则图2中水面高度为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com