
【题目】如图,在边长为1个单位长度的小正方形组成的网格中,△ABC的顶点A、B、C在小正方形的顶点上,将△ABC向下平移4个单位、再向右平移3个单位得到△A1B1C1 , 然后将△A1B1C1绕点A1顺时针旋转90°得到△A1B2C2 . 
(1)在网格中画出△A1B1C1和△A1B2C2;
(2)计算线段AC在变换到A1C2的过程中扫过区域的面积(重叠部分不重复计算)
【答案】
(1)解:如图所示:
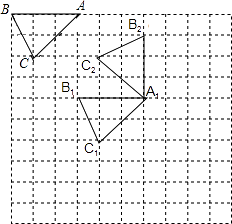
(2)解:∵图中是边长为1个单位长度的小正方形组成的网格,
∴AC= ![]() =2
=2 ![]() ,
,
∵将△ABC向下平移4个单位AC所扫过的面积是以4为底,以2为高的平行四边形的面积;再向右平移3个单位AC扫过的面积是以3为底以2为高的平行四边形的面积;当△A1B1C1绕点A1顺时针旋转90°到△A1B2C2时,A1C1所扫过的面积是以A1为圆心以2 ![]() 为半径,圆心角为90°的扇形的面积,重叠部分是以A1为圆心,以2
为半径,圆心角为90°的扇形的面积,重叠部分是以A1为圆心,以2 ![]() 为半径,圆心角为45°的扇形的面积,
为半径,圆心角为45°的扇形的面积,
∴线段AC在变换到A1C2的过程中扫过区域的面积=4×2+3×2+ ![]() ﹣
﹣ ![]() =14+π
=14+π
【解析】(1)根据图形平移及旋转的性质画出△A1B1C1及△A1B2C2即可;(2)根据图形平移及旋转的性质可知,将△ABC向下平移4个单位AC所扫过的面积是以4为底,以2为高的平行四边形的面积;再向右平移3个单位AC扫过的面积是以3为底以2为高的平行四边形的面积;当△A1B1C1绕点A1顺时针旋转90°到△A1B2C2时,A1C1所扫过的面积是以A1为圆心以以2 ![]() 为半径,圆心角为90°的扇形的面积,再减去重叠部分的面积,根据平行四边形的面积及扇形面积公式进行解答即可.
为半径,圆心角为90°的扇形的面积,再减去重叠部分的面积,根据平行四边形的面积及扇形面积公式进行解答即可.
【考点精析】利用扇形面积计算公式对题目进行判断即可得到答案,需要熟知在圆上,由两条半径和一段弧围成的图形叫做扇形;扇形面积S=π(R2-r2).


科目:初中数学 来源: 题型:
【题目】如图,已知反比例函数y= ![]() 的图象与直线y=﹣x+b都经过点A(1,4),且该直线与x轴的交点为B.
的图象与直线y=﹣x+b都经过点A(1,4),且该直线与x轴的交点为B. 
(1)求反比例函数和直线的解析式;
(2)求△AOB的面积
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=x+b(b>4)与x轴、y轴分别相交于点A、B,与反比例函数 ![]() 的图象相交于点C、D(点C在点D的左侧),⊙O是以CD长为半径的圆.CE∥x轴,DE∥y轴,CE、DE相交于点E.
的图象相交于点C、D(点C在点D的左侧),⊙O是以CD长为半径的圆.CE∥x轴,DE∥y轴,CE、DE相交于点E. 
(1)△CDE是三角形;点C的坐标为 , 点D的坐标为(用含有b的代数式表示);
(2)b为何值时,点E在⊙O上?
(3)随着b取值逐渐增大,直线y=x+b与⊙O有哪些位置关系?求出相应b的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为24cm的正方形纸片ABCD上,剪去图中阴影部分的四个全等的等腰直角三角形,再沿图中的虚线折起,折成一个长方体形状的包装盒(A、B、C、D四个顶点正好重合于上底面上一点).已知E、F在AB边上,是被剪去的一个等腰直角三角形斜边的两个端点,设AE=BF=x(cm). 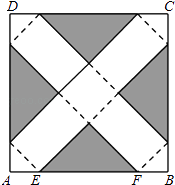
(1)若折成的包装盒恰好是个正方体,试求这个包装盒的体积V;
(2)某广告商要求包装盒的表面(不含下底面)面积S最大,试问x应取何值?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】海南有丰富的旅游产品.某校九年级(1)班的同学就部分旅游产品的喜爱情况对游客随机调查,要求游客在列举的旅游产品中选出喜爱的产品,且只能选一项.以下是同学们整理的不完整的统计图: 
根据以上信息完成下列问题:
(1)请将条形统计图补充完整;
(2)随机调查的游客有人;在扇形统计图中,A部分所占的圆心角是度;
(3)请根据调查结果估计在1500名游客中喜爱攀锦的约有人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在梯形ABCD中,已知AD∥BC,AB=CD,延长线段CB到E,使BE=AD,连接AE、AC. 
(1)求证:△ABE≌△CDA;
(2)若∠DAC=40°,求∠EAC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形OABC在平面直角坐标系中,O为坐标原点,点A(0,4),C(2,0).将矩形OABC绕点O按顺时针方向旋转135°,得到矩形EFGH(点E与O重合).
(1)若GH交y轴于点M,则∠FOM=°,OM=;
(2)将矩形EFGH沿y轴向上平移t个单位. ①直线GH与x轴交于点D,若AD∥BO,求t的值;
②若矩形EFGH与矩形OABC重叠部分的面积为S个平方单位,试求当0<t≤4 ![]() ﹣2时,S与t之间的函数关系式.
﹣2时,S与t之间的函数关系式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com