
【题目】如图,直线y=x+b(b>4)与x轴、y轴分别相交于点A、B,与反比例函数 ![]() 的图象相交于点C、D(点C在点D的左侧),⊙O是以CD长为半径的圆.CE∥x轴,DE∥y轴,CE、DE相交于点E.
的图象相交于点C、D(点C在点D的左侧),⊙O是以CD长为半径的圆.CE∥x轴,DE∥y轴,CE、DE相交于点E. 
(1)△CDE是三角形;点C的坐标为 , 点D的坐标为(用含有b的代数式表示);
(2)b为何值时,点E在⊙O上?
(3)随着b取值逐渐增大,直线y=x+b与⊙O有哪些位置关系?求出相应b的取值范围.
【答案】
(1)等腰直角;( ![]() ,
, ![]() );(
);( ![]() ,
, ![]() )
)
(2)解:当点E在⊙O上时,如图1,连接OE.
∵△CDE是等腰直角三角形,
∴E点横坐标为: ![]() ,纵坐标为:
,纵坐标为: ![]() ,
,
则OE=CD.
∵直线y=x+b与x轴、y轴相交于点A(﹣b,0),B(0,b),CE∥x轴,DE∥y轴,
∴△DCE、△AOB是等腰直角三角形.
∵整个图形是轴对称图形,
∴OE平分∠AOB,∠AOE=∠BOE=45°.
∵CE∥x轴,DE∥y轴,
∴四边形CAOE、OEDB是等腰梯形.
∴OE=AC=BD.
∵OE=CD,∴OE=AC=BD=CD.
过点C作CF⊥x轴,垂足为点F.
则△AFC∽△AOB.
∴ ![]() .
.
∴AF=CF= ![]() BO=
BO= ![]() b.
b.
∴ ![]() ,
,
解得: ![]() .
.
∵b>4,∴ ![]() .
.
∴当 ![]() 时,点E在⊙O上
时,点E在⊙O上

(3)解:当⊙O与直线y=x+b相切于点G时,
如图2,连接OG.
∵整个图形是轴对称图形,
∴点O、E、G在对称轴上.
∴GC=GD= ![]() CD=
CD= ![]() OG=
OG= ![]() AG.
AG.
∴AC=CG=GD=DB.
∴AC= ![]() AB.
AB.
过点C作CH⊥x轴,垂足为点H.
则△AHC∽△AOB.
∴ ![]() .
.
∴C的纵坐标: ![]() .
.
∴ ![]() ,
,
解得 ![]() .
.
∵b>4,∴ ![]() .
.
∴当 ![]() 时,直线y=x+b与⊙O相切;
时,直线y=x+b与⊙O相切;
当 ![]() 时,直线y=x+b与⊙O相离;
时,直线y=x+b与⊙O相离;
当 ![]() 时,直线y=x+b与⊙O相交.
时,直线y=x+b与⊙O相交.

【解析】解:(1)根据直线y=x+b(b>4)与反比例函数 ![]() 的图象相交于点C、D,CE∥x轴,DE∥y轴, 则y=x+b与y=x平行,
的图象相交于点C、D,CE∥x轴,DE∥y轴, 则y=x+b与y=x平行,
故∠DCE=45°,
则△CDE是等腰直角三角形;
将y=x+b与y=﹣ ![]() ,联立得出:
,联立得出:
x+b=﹣ ![]() ,
,
解得:x1= ![]() ,x2=
,x2= ![]() ,分别代入y=x+b得:
,分别代入y=x+b得:
y1= ![]() ,y2=
,y2= ![]() ,
,
故点C的坐标为:( ![]() ,
, ![]() ),
),
点D的坐标为:( ![]() ,
, ![]() );
);
所以答案是:等腰直角,( ![]() ,
, ![]() ),(
),( ![]() ,
, ![]() );
);


科目:初中数学 来源: 题型:
【题目】我们在学完“平移、轴对称、旋转”三种图形的变化后,可以进行进一步研究,请根据示例图形,完成下表.
图形的变化 | 示例图形 | 与对应线段有关的结论 | 与对应点有关的结论 |
平移 |
| AA′=BB′ | |
轴对称 |
| ||
旋转 |
| AB=A′B′;对应线段AB和A′B′所在的直线相交所成的角与旋转角相等或互补. |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A,B是反比例函数y= ![]() (k>0,x>0)图象上的两点,BC∥x轴,交y轴于点C,动点P从坐标原点O出发,沿O→A→B→C(图中“→”所示路线)匀速运动,终点为C,过P作PM⊥x轴,垂足为M.设三角形OMP的面积为S,P点运动时间为t,则S关于x的函数图象大致为( )
(k>0,x>0)图象上的两点,BC∥x轴,交y轴于点C,动点P从坐标原点O出发,沿O→A→B→C(图中“→”所示路线)匀速运动,终点为C,过P作PM⊥x轴,垂足为M.设三角形OMP的面积为S,P点运动时间为t,则S关于x的函数图象大致为( ) 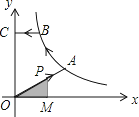
A.
B.
C.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点P在AB的延长线上,弦CE交AB于点D.连接OE、AC,且∠P=∠E,∠POE=2∠CAB.
(1)求证:CE⊥AB;
(2)求证:PC是⊙O的切线;
(3)若BD=2OD,PB=9,求⊙O的半径及tan∠P的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了进一步开展“阳光体育”活动,计划用2000元购买乒乓球拍,用2800元购买羽毛球拍.已知一副羽毛球拍比一副乒乓球拍贵14元.该校购买的乒乓球拍与羽毛球拍的数量能相同吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是使用测角仪测量一幅壁画高度的示意图,已知壁画AB的底端距离地面的高度BC=1m,在壁画的正前方点D处测得壁画底端的俯角∠BDF=30°,且点D距离地面的高度DE=2m,求壁画AB的高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 如图,△ABC中,∠ACB=90°,AB=8cm,D是AB的中点.现将△BCD沿BA方向平移1cm,得到△EFG,FG交AC于H,则GH的长等于cm. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为1个单位长度的小正方形组成的网格中,△ABC的顶点A、B、C在小正方形的顶点上,将△ABC向下平移4个单位、再向右平移3个单位得到△A1B1C1 , 然后将△A1B1C1绕点A1顺时针旋转90°得到△A1B2C2 . 
(1)在网格中画出△A1B1C1和△A1B2C2;
(2)计算线段AC在变换到A1C2的过程中扫过区域的面积(重叠部分不重复计算)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ABC=90°,点D在BC的延长线上,且BD=AB,过点B作BE⊥AC,与BD的垂线DE交于点E. 
(1)求证:△ABC≌△BDE;
(2)△BDE可由△ABC旋转得到,利用尺规作出旋转中心O(保留作图痕迹,不写作法).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com