
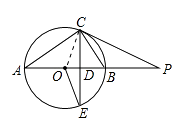
【题目】如图,AB是⊙O的直径,点P在AB的延长线上,弦CE交AB于点D.连接OE、AC,且∠P=∠E,∠POE=2∠CAB.
(1)求证:CE⊥AB;
(2)求证:PC是⊙O的切线;
(3)若BD=2OD,PB=9,求⊙O的半径及tan∠P的值.
【答案】
(1)
证明:连接OC,
∴∠COB=2∠CAB,
又∠POE=2∠CAB.
∴∠COD=∠EOD,
则弧BC=弧BE,
即CE⊥AB;
(2)
证明:∵CE⊥AB,∠P=∠E,
∴∠P+∠PCD=∠E+∠PCD=90°,
又∠OCD=∠E,
∴∠OCD+∠PCD=∠PCO=90°,
∴PC是⊙O的切线;
(3)
解:设⊙O的半径为r,OD=x,则BD=2x,r=3x,
∵CD⊥OP,OC⊥PC,
∴Rt△OCD∽Rt△OPC,
∴OC2=ODOP,即(3x)2=x(3x+9),
解之得x= ![]() ,
,
∴⊙O的半径r= ![]() ,
,
在Rt△OCP中, PC= ![]() =
= ![]() =9
=9 ![]() ,
,
tan∠P= ![]() =
= ![]() .
.
【解析】(1)此题方法不唯一,主要是运用“同弧所对的圆周角是圆心角的一半”,题中给出的是证明弧BC和弧BE所对的圆心角相等,则所对的弧相等,则由垂径定理可证得;
2)证明相切,需证明半径OC⊥CP,即证明∠PCO=90°;而由(1)可得∠P+∠PCD=∠E+∠PCD=90°,而由半径OE=OC,根据等边对等角,可得∠OCD=∠E,则可证得∠OCD+∠PCD=∠PCO=90°;
3)要求⊙O的半径,可考虑运用勾股定理的方法和相似三角形的方法,题中给出的是运用相似三角形的判定和性质解答,由BD=2OD,可得边BD,半径与OD的关系,则证明Rt△OCD∽Rt△OPC,可得边 OC2=ODOP,代入相关数据,求出半径OC和OD;在Rt△OCP中,tan∠P= ![]() ,OC已求,则PO=OB+PB,则可求出PC,代入即可解出.
,OC已求,则PO=OB+PB,则可求出PC,代入即可解出.
【考点精析】关于本题考查的勾股定理的概念和切线的性质定理,需要了解直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径才能得出正确答案.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,已知反比例函数y= ![]() 的图象与直线y=﹣x+b都经过点A(1,4),且该直线与x轴的交点为B.
的图象与直线y=﹣x+b都经过点A(1,4),且该直线与x轴的交点为B. 
(1)求反比例函数和直线的解析式;
(2)求△AOB的面积
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标中,△ABC三个顶点坐标为A(﹣ ![]() ,0)、B(
,0)、B( ![]() ,0)、C(0,3).
,0)、C(0,3). 
(1)求△ABC内切圆⊙D的半径.
(2)过点E(0,﹣1)的直线与⊙D相切于点F(点F在第一象限),求直线EF的解析式.
(3)以(2)为条件,P为直线EF上一点,以P为圆心,以2 ![]() 为半径作⊙P.若⊙P上存在一点到△ABC三个顶点的距离相等,求此时圆心P的坐标.
为半径作⊙P.若⊙P上存在一点到△ABC三个顶点的距离相等,求此时圆心P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=x+b(b>4)与x轴、y轴分别相交于点A、B,与反比例函数 ![]() 的图象相交于点C、D(点C在点D的左侧),⊙O是以CD长为半径的圆.CE∥x轴,DE∥y轴,CE、DE相交于点E.
的图象相交于点C、D(点C在点D的左侧),⊙O是以CD长为半径的圆.CE∥x轴,DE∥y轴,CE、DE相交于点E. 
(1)△CDE是三角形;点C的坐标为 , 点D的坐标为(用含有b的代数式表示);
(2)b为何值时,点E在⊙O上?
(3)随着b取值逐渐增大,直线y=x+b与⊙O有哪些位置关系?求出相应b的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为24cm的正方形纸片ABCD上,剪去图中阴影部分的四个全等的等腰直角三角形,再沿图中的虚线折起,折成一个长方体形状的包装盒(A、B、C、D四个顶点正好重合于上底面上一点).已知E、F在AB边上,是被剪去的一个等腰直角三角形斜边的两个端点,设AE=BF=x(cm). 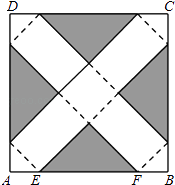
(1)若折成的包装盒恰好是个正方体,试求这个包装盒的体积V;
(2)某广告商要求包装盒的表面(不含下底面)面积S最大,试问x应取何值?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com