
【题目】如图,半径为1的半圆形纸片,按如图方式折叠,使对折后圆弧的中点M与圆心O重合,则图中阴影部分的面积是.
【答案】![]()
【解析】解:如图,连接OM,交弦AB于C,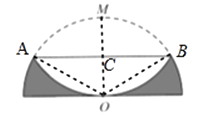
由题意知,OM⊥AB,且OC=MC= ![]() ,
,
在Rt△AOC中,∵OA=1,OC= ![]() ,
,
∴cos∠AOC= ![]() =
= ![]() ,AC=
,AC= ![]() =
= ![]() ,
,
∴∠AOC=60°,AB=2AC= ![]() ,
,
∴∠AOB=2∠AOC=120°,
则S弓形ABM=S扇形OAB-S△AOB= ![]() -
- ![]() ×
× ![]() ×
× ![]() =
= ![]() ,
,
则S阴影= S半圆-2S弓形ABM= ![]() π×12-2(
π×12-2( ![]() )=
)= ![]() .
.
故答案为 ![]() .
.
分割图形可知阴影部分的面积就等于S半圆-2S弓形ABM , 圆的半径已知,则只需要求出S弓形ABM=S扇形OAB-S△AOB , 要S扇形OAB的面积,则必要求出圆心角∠AOB,则∠AOC必是特殊角;根据折叠可得OC=MC,且OM⊥AB,由垂径定理可得AC=BC,在Rt△AOC中,OA=1,OC= ![]() ,则可得∠AOC=60°,及AC的边长,即可解答.
,则可得∠AOC=60°,及AC的边长,即可解答.


 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD内接于⊙O,F是 ![]() 上一点,且
上一点,且 ![]() =
= ![]() ,连接CF并延长交AD的延长线于点E,连接AC.若∠ABC=105°,∠BAC=25°,则∠E的度数为( )
,连接CF并延长交AD的延长线于点E,连接AC.若∠ABC=105°,∠BAC=25°,则∠E的度数为( )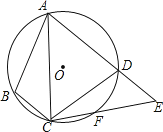
A.45°
B.50°
C.55°
D.60°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学活动﹣旋转变换
(1)如图①,在△ABC中,∠ABC=130°,将△ABC绕点C逆时针旋转50°得到△A′B′C,连接BB′,求∠A′B′B的大小;
(2)如图②,在△ABC中,∠ABC=150°,AB=3,BC=5,将△ABC绕点C逆时针旋转60°得到△A′B′C,连接BB′,以A′为圆心,A′B′长为半径作圆.
①猜想:直线BB′与⊙A′的位置关系,并证明你的结论;
②连接A′B,求线段A′B的长度;
(3)如图③,在△ABC中,∠ABC=α(90°<α<180°),AB=m,BC=n,将△ABC绕点C逆时针旋转2β角度(0°<2β<180°)得到△A′B′C,连接A′B和BB′,以A′为圆心,A′B′长为半径作圆,问:角α与角β满足什么条件时,直线BB′与⊙A′相切,请说明理由,并求此条件下线段A′B的长度(结果用角α或角β的三角函数及字母m、n所组成的式子表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A,B是反比例函数y= ![]() (k>0,x>0)图象上的两点,BC∥x轴,交y轴于点C,动点P从坐标原点O出发,沿O→A→B→C(图中“→”所示路线)匀速运动,终点为C,过P作PM⊥x轴,垂足为M.设三角形OMP的面积为S,P点运动时间为t,则S关于x的函数图象大致为( )
(k>0,x>0)图象上的两点,BC∥x轴,交y轴于点C,动点P从坐标原点O出发,沿O→A→B→C(图中“→”所示路线)匀速运动,终点为C,过P作PM⊥x轴,垂足为M.设三角形OMP的面积为S,P点运动时间为t,则S关于x的函数图象大致为( ) 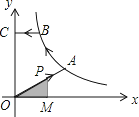
A.
B.
C.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的有( )
①面积之比为1:2的两个相似三角形的周长之比是1:4;②三视图相同的几何体是正方形;③-27没有立方根;④对角线互相垂直的四边形是菱形;⑤某中学人数相等的甲、乙两班学生参加了同一次数学测验,班平均分和方差分别为 ![]() =82分,
=82分, ![]() =82分,
=82分, ![]() =245,
=245, ![]() =190,那么成绩较为整齐的是乙班,
=190,那么成绩较为整齐的是乙班,
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点P在AB的延长线上,弦CE交AB于点D.连接OE、AC,且∠P=∠E,∠POE=2∠CAB.
(1)求证:CE⊥AB;
(2)求证:PC是⊙O的切线;
(3)若BD=2OD,PB=9,求⊙O的半径及tan∠P的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了进一步开展“阳光体育”活动,计划用2000元购买乒乓球拍,用2800元购买羽毛球拍.已知一副羽毛球拍比一副乒乓球拍贵14元.该校购买的乒乓球拍与羽毛球拍的数量能相同吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 如图,△ABC中,∠ACB=90°,AB=8cm,D是AB的中点.现将△BCD沿BA方向平移1cm,得到△EFG,FG交AC于H,则GH的长等于cm. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】线段MN在直角坐标系中的位置如图所示,若线段M′N′与MN关于y轴对称,则点M的对应点M′的坐标为( )
A.(4,2)
B.(﹣4,2)
C.(﹣4,﹣2)
D.(4,﹣2)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com