
【题目】如图是使用测角仪测量一幅壁画高度的示意图,已知壁画AB的底端距离地面的高度BC=1m,在壁画的正前方点D处测得壁画底端的俯角∠BDF=30°,且点D距离地面的高度DE=2m,求壁画AB的高度.
【答案】解:先过点B作BG⊥DE于点G.
∵DE⊥CE,EC⊥CF,DF⊥AC,
∴四边形DECF是矩形,
∵BC=1m,DE=2m,
∴EG=BC=1m,DG=BF=1m,
在Rt△DBF中,
∵∠BDF=30°,BF=1m,
∴DF= ![]() =
= ![]() =
= ![]() ,
,
同理,在Rt△ADF中,
∵∠ADF=60°,DF= ![]() ,
,
∴AF=DFtan60°= ![]() ×
× ![]() =3m.
=3m.
∴AB=AF+BF=3+1=4m.
答:壁画AB的高度是4米.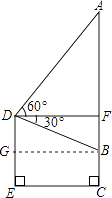
【解析】先过点B作BG⊥DE于点G,由于DE⊥CE,EC⊥CE,DF⊥AC,故四边形DECF是矩形,BC=1m,DE=2m,所以EG=BC=1m,故DG=BF=1m,在Rt△DBF中,由锐角三角函数的定义可求出DF的长,同理在Rt△ADF中由锐角三角函数的定义可求出AF的长,根据AB=AF+BF即可得出结论.
【考点精析】关于本题考查的锐角三角函数的定义,需要了解锐角A的正弦、余弦、正切、余切都叫做∠A的锐角三角函数才能得出正确答案.


 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案科目:初中数学 来源: 题型:
【题目】图中是抛物线拱桥,P处有一照明灯,水面OA宽4m,从O、A两处观测P处,仰角分别为α、β,且tanα= ![]() ,
, ![]() ,以O为原点,OA所在直线为x轴建立直角坐标系.
,以O为原点,OA所在直线为x轴建立直角坐标系.
(1)求点P的坐标;
(2)水面上升1m,水面宽多少( ![]() 取1.41,结果精确到0.1m)?
取1.41,结果精确到0.1m)?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标中,△ABC三个顶点坐标为A(﹣ ![]() ,0)、B(
,0)、B( ![]() ,0)、C(0,3).
,0)、C(0,3). 
(1)求△ABC内切圆⊙D的半径.
(2)过点E(0,﹣1)的直线与⊙D相切于点F(点F在第一象限),求直线EF的解析式.
(3)以(2)为条件,P为直线EF上一点,以P为圆心,以2 ![]() 为半径作⊙P.若⊙P上存在一点到△ABC三个顶点的距离相等,求此时圆心P的坐标.
为半径作⊙P.若⊙P上存在一点到△ABC三个顶点的距离相等,求此时圆心P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=x+b(b>4)与x轴、y轴分别相交于点A、B,与反比例函数 ![]() 的图象相交于点C、D(点C在点D的左侧),⊙O是以CD长为半径的圆.CE∥x轴,DE∥y轴,CE、DE相交于点E.
的图象相交于点C、D(点C在点D的左侧),⊙O是以CD长为半径的圆.CE∥x轴,DE∥y轴,CE、DE相交于点E. 
(1)△CDE是三角形;点C的坐标为 , 点D的坐标为(用含有b的代数式表示);
(2)b为何值时,点E在⊙O上?
(3)随着b取值逐渐增大,直线y=x+b与⊙O有哪些位置关系?求出相应b的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一个数值转换器.

(1)当输入x=25时,求输出的y的值;
(2)是否存在输入x的值后,始终输不出y的值?如果存在,请直接写出所有满足要求的x值;如果不存在,请说明理由;
(3)输入一个两位数x,恰好经过三次取算术平方根才能输出无理数y,则x=________(只填一个即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为24cm的正方形纸片ABCD上,剪去图中阴影部分的四个全等的等腰直角三角形,再沿图中的虚线折起,折成一个长方体形状的包装盒(A、B、C、D四个顶点正好重合于上底面上一点).已知E、F在AB边上,是被剪去的一个等腰直角三角形斜边的两个端点,设AE=BF=x(cm). 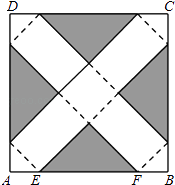
(1)若折成的包装盒恰好是个正方体,试求这个包装盒的体积V;
(2)某广告商要求包装盒的表面(不含下底面)面积S最大,试问x应取何值?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】海南有丰富的旅游产品.某校九年级(1)班的同学就部分旅游产品的喜爱情况对游客随机调查,要求游客在列举的旅游产品中选出喜爱的产品,且只能选一项.以下是同学们整理的不完整的统计图: 
根据以上信息完成下列问题:
(1)请将条形统计图补充完整;
(2)随机调查的游客有人;在扇形统计图中,A部分所占的圆心角是度;
(3)请根据调查结果估计在1500名游客中喜爱攀锦的约有人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某月的日历表,在此日历表上可以用一个矩形圈出3×3个位置的9个数(如6,7,8,13,14,15,20,21,22).若圈出的9个数中,最大数与最小数的和为42,则这9个数的和为( )

A. 69 B. 84 C. 189 D. 207
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com