
【题目】如图是某月的日历表,在此日历表上可以用一个矩形圈出3×3个位置的9个数(如6,7,8,13,14,15,20,21,22).若圈出的9个数中,最大数与最小数的和为42,则这9个数的和为( )

A. 69 B. 84 C. 189 D. 207
【答案】C
【解析】
由日历表可知,圈出的9个数中,最大数与最小数的差总为16,故圈出的最小数为x,则圈出的最大数为x+16;
接下来根据圈出的9个数中最大数与最小数的和为42可列方程,求解即可得到圈出最小数;
此时再根据圈出的9个数中,每一行相邻两数相差1,每一列相邻两数相差7即可写出这9个数,至此,本题就不难解答了.
解:设圈出的最小数为x,则圈出的最大数为x+16,由题意得,
x+(x+16)=42,
解得x=13.
故圈出的最小的三个数为13,14,15,
下面一行的数分别比上面三个数大7,故为20,21,22,
第三行的数分别比上一行三个数大7,故为27,28,29,
所以圈出的这9个数的和为189.


 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:初中数学 来源: 题型:
【题目】如图是使用测角仪测量一幅壁画高度的示意图,已知壁画AB的底端距离地面的高度BC=1m,在壁画的正前方点D处测得壁画底端的俯角∠BDF=30°,且点D距离地面的高度DE=2m,求壁画AB的高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y= ![]() x2﹣
x2﹣ ![]() (b+1)x+
(b+1)x+ ![]() (b是实数且b>2)与x轴的正半轴分别交于点A、B(点A位于点B的左侧),与y轴的正半轴交于点C.
(b是实数且b>2)与x轴的正半轴分别交于点A、B(点A位于点B的左侧),与y轴的正半轴交于点C.
(1)点B的坐标为 , 点C的坐标为(用含b的代数式表示);
(2)请你探索在第一象限内是否存在点P,使得四边形PCOB的面积等于2b,且△PBC是以点P为直角顶点的等腰直角三角形?如果存在,求出点P的坐标;如果不存在,请说明理由;
(3)请你进一步探索在第一象限内是否存在点Q,使得△QCO,△QOA和△QAB中的任意两个三角形均相似(全等可作相似的特殊情况)?如果存在,求出点Q的坐标;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】菱形ABCD中,∠B=60°,点E在边BC上,点F在边CD上.
(1)如图1,若E是BC的中点,∠AEF=60°,求证:BE=DF; 
(2)如图2,若∠EAF=60°,求证:△AEF是等边三角形. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ABC=90°,点D在BC的延长线上,且BD=AB,过点B作BE⊥AC,与BD的垂线DE交于点E. 
(1)求证:△ABC≌△BDE;
(2)△BDE可由△ABC旋转得到,利用尺规作出旋转中心O(保留作图痕迹,不写作法).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣x2+bx+c与x轴交于A、B两点,与y轴交于点C,点O为坐标原点,点D为抛物线的顶点,点E在抛物线上,点F在x轴上,四边形OCEF为矩形,且OF=2,EF=3,
(1)求抛物线所对应的函数解析式;
(2)求△ABD的面积;
(3)将△AOC绕点C逆时针旋转90°,点A对应点为点G,问点G是否在该抛物线上?请说明理由.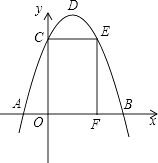
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知反比例函数y= ![]() (k1>0),y=
(k1>0),y= ![]() (k2<0).点A在y轴的正半轴上,过点A作直线BC∥x轴,且分别与两个反比例函数的图象交于点B和C,连接OC、OB.若△BOC的面积为
(k2<0).点A在y轴的正半轴上,过点A作直线BC∥x轴,且分别与两个反比例函数的图象交于点B和C,连接OC、OB.若△BOC的面积为 ![]() ,AC:AB=2:3,则k1= , k2= .
,AC:AB=2:3,则k1= , k2= . 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com