
【题目】菱形ABCD中,∠B=60°,点E在边BC上,点F在边CD上.
(1)如图1,若E是BC的中点,∠AEF=60°,求证:BE=DF; 
(2)如图2,若∠EAF=60°,求证:△AEF是等边三角形. 
【答案】
(1)证明:连接AC,
∵在菱形ABCD中,∠B=60°,
∴AB=BC=CD,∠C=180°﹣∠B=120°,
∴△ABC是等边三角形,
∵E是BC的中点,
∴AE⊥BC,
∵∠AEF=60°,
∴∠FEC=90°﹣∠AEF=30°,
∴∠CFE=180°﹣∠FEC﹣∠ECF=180°﹣30°﹣120°=30°,
∴∠FEC=∠CFE,
∴EC=CF,
∴BE=DF

(2)证明:∵△ABC是等边三角形,
∴AB=AC,∠ACB=60°,
∴∠B=∠ACF=60°,
∵AD∥BC,
∴∠AEB=∠EAD=∠EAF+∠FAD=60°+∠FAD,
∠AFC=∠D+∠FAD=60°+∠FAD,
∴∠AEB=∠AFC,
在△ABE和△ACF中,

∴△ABE≌△ACF(AAS),
∴AE=AF,
∵∠EAF=60°,
∴△AEF是等边三角形

【解析】(1)首先连接AC,由菱形ABCD中,∠B=60°,根据菱形的性质,易得△ABC是等边三角形,又由三线合一,可证得AE⊥BC,继而求得∠FEC=∠CFE,即可得EC=CF,继而证得BE=DF;(2)首先由△ABC是等边三角形,即可得AB=AC,以求得∠ACF=∠B=60°,然后利用平行线与三角形外角的性质,可求得∠AEB=∠AFC,证得△AEB≌△AFC,即可得AE=AF,证得:△AEF是等边三角形.
【考点精析】通过灵活运用等边三角形的判定和菱形的性质,掌握三个角都相等的三角形是等边三角形;有一个角等于60°的等腰三角形是等边三角形;菱形的四条边都相等;菱形的对角线互相垂直,并且每一条对角线平分一组对角;菱形被两条对角线分成四个全等的直角三角形;菱形的面积等于两条对角线长的积的一半即可以解答此题.


科目:初中数学 来源: 题型:
【题目】海南有丰富的旅游产品.某校九年级(1)班的同学就部分旅游产品的喜爱情况对游客随机调查,要求游客在列举的旅游产品中选出喜爱的产品,且只能选一项.以下是同学们整理的不完整的统计图: 
根据以上信息完成下列问题:
(1)请将条形统计图补充完整;
(2)随机调查的游客有人;在扇形统计图中,A部分所占的圆心角是度;
(3)请根据调查结果估计在1500名游客中喜爱攀锦的约有人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解答题
(1)如图(1)点P是正方形ABCD的边CD上一点(点P与点C,D不重合),点E在BC的延长线上,且CE=CP,连接BP,DE.求证:△BCP≌△DCE; 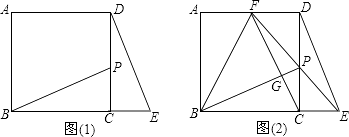
(2)直线EP交AD于F,连接BF,FC.点G是FC与BP的交点. ①若CD=2PC时,求证:BP⊥CF;
②若CD=nPC(n是大于1的实数)时,记△BPF的面积为S1 , △DPE的面积为S2 . 求证:S1=(n+1)S2 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某月的日历表,在此日历表上可以用一个矩形圈出3×3个位置的9个数(如6,7,8,13,14,15,20,21,22).若圈出的9个数中,最大数与最小数的和为42,则这9个数的和为( )

A. 69 B. 84 C. 189 D. 207
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场将进价为2000元的冰箱以2400元售出,平均每天能售出8台,为了配合国家“家电下乡”政策的实施,商场决定采取适当的降价措施.调查表明:这种冰箱的售价每降低50元,平均每天就能多售出4台.
(1)假设每台冰箱降价x元,商场每天销售这种冰箱的利润是y元,请写出y与x之间的函数表达式;(不要求写自变量的取值范围)
(2)商场要想在这种冰箱销售中每天盈利4800元,同时又要使百姓得到实惠,每台冰箱应降价多少元?
(3)每台冰箱降价多少元时,商场每天销售这种冰箱的利润最高?最高利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com