
【题目】某商场将进价为2000元的冰箱以2400元售出,平均每天能售出8台,为了配合国家“家电下乡”政策的实施,商场决定采取适当的降价措施.调查表明:这种冰箱的售价每降低50元,平均每天就能多售出4台.
(1)假设每台冰箱降价x元,商场每天销售这种冰箱的利润是y元,请写出y与x之间的函数表达式;(不要求写自变量的取值范围)
(2)商场要想在这种冰箱销售中每天盈利4800元,同时又要使百姓得到实惠,每台冰箱应降价多少元?
(3)每台冰箱降价多少元时,商场每天销售这种冰箱的利润最高?最高利润是多少?
【答案】
(1)解:根据题意,得y=(2400﹣2000﹣x)(8+4× ![]() ),
),
即y=﹣ ![]() x2+24x+3200
x2+24x+3200
(2)解:由题意,得﹣ ![]() x2+24x+3200=4800.
x2+24x+3200=4800.
整理,得x2﹣300x+20000=0.
解这个方程,得x1=100,x2=200.
要使百姓得到实惠,取x=200元.
∴每台冰箱应降价200元
(3)解:对于y=﹣ ![]() x2+24x+3200=﹣
x2+24x+3200=﹣ ![]() (x﹣150)2+5000,
(x﹣150)2+5000,
当x=150时,
y最大值=5000(元).
所以,每台冰箱的售价降价150元时,商场的利润最大,最大利润是5000元
【解析】(1)根据题意易求y与x之间的函数表达式.(2)已知函数解析式,设y=4800可从实际得x的值.(3)利用x=﹣ ![]() 求出x的值,然后可求出y的最大值.
求出x的值,然后可求出y的最大值.


科目:初中数学 来源: 题型:
【题目】数轴上,A、B两点表示的数a,b满足|a﹣6|+(b+12)2=0
(1)a= ,b= ;
(2)若小球M从A点向负半轴运动、小球N从B点向正半轴运动,两球同时出发,小球M运动的速度为每秒2个单位,当M运动到OB的中点时,N点也同时运动到OA的中点,则小球N的速度是每秒 个单位;
(3)若小球M、N保持(2)中的速度,分别从A、B两点同时出发,经过 秒后两个小球相距两个单位长度.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
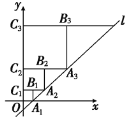
【题目】如图:在平面直角坐标系中,直线l:![]() 与x轴交于点A1,如图所示依次作正方形A1B1C1O、
与x轴交于点A1,如图所示依次作正方形A1B1C1O、
正方形A2B2C2C1、…、正方形![]() ,使得点A1、A2、A3、…在直线l上,点C1、C2、C3、…
,使得点A1、A2、A3、…在直线l上,点C1、C2、C3、…
在y轴正半轴上,则点![]() 的坐标是_______________________.
的坐标是_______________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明身高为1.6米,通过地面上的一块平面镜C,刚好能看到前方大树的树梢E,此时他测得俯角为45度,然后他直接抬头观察树梢E,测得仰角为30度.求树的高度.(结果保留根号) 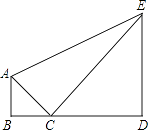
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,点C在线段AB上,且AC=6cm,BC=14cm,点M、N分别是AC、BC的中点.
![]()
(1)求线段MN的长度;
(2)在(1)中,如果AC=acm,BC=bcm,其它条件不变,你能猜测出MN的长度吗?请说出你发现的结论,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列各式:
13+23=1+8=9,而(1+2)2=9,∴13+23=(1+2)2;
13+23+33=36,而(1+2+3)2=36,∴13+23+33=(1+2+3)2;
13+23+33+43=100,而(1+2+3+4)2=100,∴13+23+33+43=(1+2+3+4)2;
∴13+23+33+43+53=(______ )2= ______ .
根据以上规律填空:
(1)13+23+33+…+n3=(______ )2=[ ______ ]2.
(2)猜想:113+123+133+143+153= ______ .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校为了解学生对新闻、体育、动画、娱乐、戏曲五类电视节目最喜爱的情况,随机调查了若干名学生,根据调查数据进行整理,绘制了如下的不完整统计图. 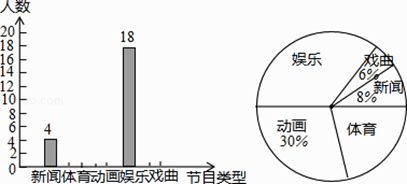
请你根据以上的信息,回答下列问题:
(1)本次共调查了名学生,其中最喜爱戏曲的有人;在扇形统计图中,最喜爱体育的对应扇形的圆心角大小是 .
(2)根据以上统计分析,估计该校2000名学生中最喜爱新闻的人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com