
一个等边三角形的对称轴有__________条.
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
三等分任意角是三大几何作图不能问题之一,古希腊数学家阿基米德就设计 出了一个巧妙的三等分角的方法:在直尺边缘上添加一点P,命尺端为O(如图①);设所要三等分的角是∠MCN,以C为圆心,OP为半径作半圆交给定角的两边CM、CN于A、B两点;移动直尺,使直尺上的O点在AC的延长线上移动,P点在圆周上移动,当直尺正好通过B点时,连OPB,则有∠AOB=
出了一个巧妙的三等分角的方法:在直尺边缘上添加一点P,命尺端为O(如图①);设所要三等分的角是∠MCN,以C为圆心,OP为半径作半圆交给定角的两边CM、CN于A、B两点;移动直尺,使直尺上的O点在AC的延长线上移动,P点在圆周上移动,当直尺正好通过B点时,连OPB,则有∠AOB= ∠MCN.这种方法由于在直尺上作了一个记号,不符合尺规作图中直尺只能用来连线的规定,因此还不能算是严格意义上的尺规作图.
∠MCN.这种方法由于在直尺上作了一个记号,不符合尺规作图中直尺只能用来连线的规定,因此还不能算是严格意义上的尺规作图.
(1)动手实践操作,用以上方法三等分∠MCN,在图② 中画出图形并
中画出图形并 标明相应字母;
标明相应字母;
(2)请你就阿基米德的作图方法给出证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
.如图,△ABC是等边三角形,D为BC边上一个动点(D与B、C均不重合),AD=AE,∠DAE=60°,连接CE.
(1)求证:△ABD≌△ACE;
(2)求证:CE平分∠ACF;
(3)若AB=2,当四边形ADCE的周长取最小值时,求BD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
已知:a、b、c为△ABC的三边,且满足a2c2﹣b2c2=a4﹣b4,试判断△ABC的形状.
解:∵a2c2﹣b2c2=a4﹣b4,①
∴c2(a2﹣b2)=(a2+b2)(a2﹣b2).②
∴c2=a2+b2.③
∴△ABC是直角三角形.
问:
(1)在上述解题过程中,从哪一步开始出现错误?请写出该步的代号:__________;
(2)错误的原因为__________;
(3)本题正确的解题过程:
查看答案和解析>>
科目:初中数学 来源: 题型:
“黄金1号”玉米种子的价格为5元/千克,如果一次购买2千克以上的种子,超过2千克部分的种子价格打6折,设购买种子数量为x千克,付款金额为y元,则y与x的函数关系的图象大致是( )
A. B.
B.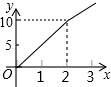 C.
C.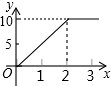 D.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com