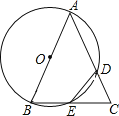
【题目】已知△ABC，以AB为直径的⊙O分别交AC于D，BC于E，连接ED，若ED=EC．
（1）求证：AB=AC；
（2）若AB=4，BC=
，求CD的长．
【答案】（1）证明过程见解析；（2）
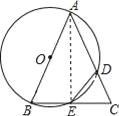
【解析】试题分析：（1）由等腰三角形的性质得到∠EDC=∠C，由圆外接四边形的性质得到∠EDC=∠B，由此推得∠B=∠C，由等腰三角形的判定即可证得结论；（2）连接AE，由AB为直径，可证得AE⊥BC，由（1）知AB=AC，由“三线合一”定理得到BE=CE=
BC=
，由割线定理可证得结论．
试题解析：（1）∵ED=EC， ∴∠EDC=∠C， ∵∠EDC=∠B， ∴∠B=∠C， ∴AB=AC；
（2）连接AE， ∵AB为直径， ∴AE⊥BC， 由（1）知AB=AC， ∴BE=CE=BC=，
∵CECB=CDCA，AC=AB=4， ∴2=4CD， ∴CD=
．
黄冈天天练口算题卡系列答案科目：初中数学 来源： 题型：
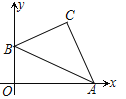
【题目】在平面直角坐标系中，已知点A、B的坐标分别为
A（6，0）、B（0，2），以AB为斜边在右上方作Rt△ABC.设点C坐标为（x，y），则（x+y）的最大值为__．
查看答案和解析>>
科目：初中数学 来源： 题型：
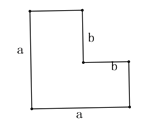
【题目】如图“L”形图形的面积有如下四种表示方法：①a2－b2；
②a（a－b）＋b（a－b）；③（a＋b）（a－b）；④（a－b）2．其中正确
的表示方法有（ ）
A. 1种 B. 2种 C. 3种 D. 4种
查看答案和解析>>
科目：初中数学 来源： 题型：
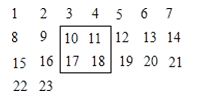
【题目】把2100个连续的正整数1、2、3、……、2100，按如图方式排列成一个数表，如图用一个正方形框在表中任意框住4个数，设左上角的数为x．
（1） 另外三个数用含x的式子表示出来，从小到大排列是___________
（2） 被框住4个数的和为416时，x值为多少？
（3） 能否框住四个数和为324？若能，求出x值；若不能，说明理由
（4） 从左到右，第1至第7列各数之和分别为a1、a2、a3、a4、a5、a6、a7，请直接写出7个数中最大的数与最小的数之差．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】问题探究：
（1）如图①，边长为4的等边△OAB位于平面直角坐标系中，将△OAB折叠，使点B落在OA的中点处，则折痕长为 ；
（2）如图②，矩形OABC位于平面直角坐标系中，其中OA=8，AB=6，将矩形沿线段MN折叠，点B落在x轴上，其中AN=
AB，求折痕MN的长；
问题解决：
（3）如图③，四边形OABC位于平面直角坐标系中，其中OA=AB=6，CB=4，BC∥OA，AB⊥OA于点A，点Q（4，3）为四边形内部一点，将四边形折叠，使点B落在x轴上，问是否存在过点Q的折痕，若存在，求出折痕长，若不存在，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知某种纸一张的厚度约为0.0089cm，用科学记数法表示这个数为（ ）
A.8.9×103
B.8.9×10﹣4
C.8.9×10﹣3
D.89×10﹣2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com