
【题目】问题探究:
(1)如图①,边长为4的等边△OAB位于平面直角坐标系中,将△OAB折叠,使点B落在OA的中点处,则折痕长为 ;
(2)如图②,矩形OABC位于平面直角坐标系中,其中OA=8,AB=6,将矩形沿线段MN折叠,点B落在x轴上,其中AN=![]() AB,求折痕MN的长;
AB,求折痕MN的长;
问题解决:
(3)如图③,四边形OABC位于平面直角坐标系中,其中OA=AB=6,CB=4,BC∥OA,AB⊥OA于点A,点Q(4,3)为四边形内部一点,将四边形折叠,使点B落在x轴上,问是否存在过点Q的折痕,若存在,求出折痕长,若不存在,请说明理由.

【答案】(1)2;
(2)MN的长为![]() .
.
(3)折痕的长为5或![]() .
.
【解析】(1)如图1中,B的对称点B/,折痕为MN,MN交BB/于H. 只要证明折痕是△ABC的中位线即可.
(2)如图2中,B的对称点B/,折痕为MN,MN交BB/于H,求出直线MN的解析式即可解决问题.
(3)存在. 如图3中,延长BQ交OA于B//,连接AQ,过点作Q作MN∥OA,交OC于M,交AB于N,可以证明线段MN计算折痕;作BB//的垂直平分线PF,交OC于P,交AB于F,此时B、B//关于直线PF对称,线段PF也是折痕,分别求出MN、PF即可解决问题.
解:(1)如图1中,B的对称点B′,
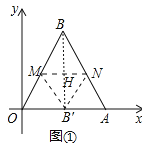
折痕为MN,MN交BB′于H.
∵△ABC是等边三角形,OB′=B′A,∴BB′⊥OA,又∵BB′⊥MN,
∴MN∥OA,∵BH=HB′,∴BM=OM,BN=NA,
∴MN是△ABC的中位线,∴MN=![]() OA=2.故答案为2.
OA=2.故答案为2.
(2)如图2中,B的对称点B′,折痕为MN,MN交BB′于H
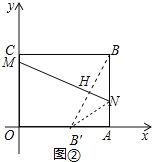
∵AN=![]() AB=2,∴NB=NB′=4,
AB=2,∴NB=NB′=4,
在Rt△ANB′中,AB′=![]() =2
=2![]() ,∴OB′=8﹣2
,∴OB′=8﹣2![]() ,
,
∴点B′(8﹣2![]() ,0),∵B(8,6),
,0),∵B(8,6),
∴BB′中点H(8﹣![]() ,3),∵点N坐标(8,2),
,3),∵点N坐标(8,2),
设直线NH解析式为y=kx+b,则有![]() 解得
解得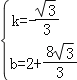 ,
,
∴直线NH解析式为y=﹣![]() x+2+
x+2+![]() ,∴点M坐标(0,2+
,∴点M坐标(0,2+![]() ),
),
∴MN=![]() =
=![]() .
.

(3)存在.理由:如图3中,延长BQ交OA于B″,连接AQ,过点Q作MN∥OA,交OC于M,交AB于N.
∵Q(4,3),∴N(6,3),∴BN=AN.QB=QB″,
作BB″的垂直平分线PF,交OC于P,交AB于F,此时B、B″关于直线PF对称,满足条件,
在Rt△ABB″中,∵∠BAB″=90°,BQ=QB″,∴AQ=QB,
∴此时B、A(B′)关于直线MN对称,满足条件.∵C(2,6),
∴直线OC解析式为y=3x,∵NM∥OA,BN=NA,∴CM=OM,∴点M(1,3),
∴MN=5,∵B(6,6),B″(2,0),∴可得直线BB″的解析式为y=![]() x﹣3,
x﹣3,
∴过点Q垂直BB″的直线PF的解析式为y=﹣![]() x+
x+![]() ,
,
由 解得
解得![]() ,∴点P(
,∴点P(![]() ,
,![]() ),F(6,
),F(6,![]() ),
),
∴PF=![]() =
=![]() ,综上所述,折痕的长为5或
,综上所述,折痕的长为5或![]() .
.
“点睛”本题考查四边形综合题、一次函数、勾股定理、线段垂直平分线性质,两条直线垂直k的乘积为-1等知识,解题的关键是灵活待定系数法确定函数解析式,学会利用解方程组求两个函数的交点坐标,属于中考压轴题.


科目:初中数学 来源: 题型:
【题目】某商场试销一种成本为50元/件的![]() 恤.经试销发现,销售量
恤.经试销发现,销售量![]() (件)与销售单价
(件)与销售单价![]() (元/件)符合一次函数关系,试销数据如下表:
(元/件)符合一次函数关系,试销数据如下表:
售价(元/件) | …… | 55 | 60 | 70 | …… |
销量(件) | …… | 75 | 70 | 60 | …… |
(1)求一次函数![]() 的表达式;
的表达式;
(2)若该商场获得利润为W元,试写出利润W与销售单价![]() 之间的关系式;销售单价定为多少时,商场可获得最大利润,最大利润是多少?
之间的关系式;销售单价定为多少时,商场可获得最大利润,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在纸上画了一条数轴后,折叠纸面,使数轴上表示1的点与表示﹣3的点重合,此时点A与点B也重合,若数轴上A、B两点之间的距离为2018(A在B的左侧),则A点表示的数为( )
A. ﹣1008 B. ﹣1009 C. ﹣1010 D. ﹣1011
查看答案和解析>>
科目:初中数学 来源: 题型:
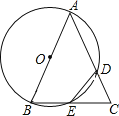
【题目】已知△ABC,以AB为直径的⊙O分别交AC于D,BC于E,连接ED,若ED=EC.
(1)求证:AB=AC;
(2)若AB=4,BC=![]() ,求CD的长.
,求CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某中学有一块四边形的空地ABCD,学校计划在空地上种植草皮,经测量∠A=90°,AB=3m,BC=12m,CD=13m,DA=4m,若每平方米草皮需要200元,问学校需要投入多少资金买草皮? 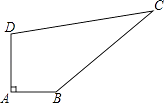
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为调查某班学生每天使用零花钱的情况,张华随机调查了30名同学,结果如下表:
每天使用零花钱(单位:元) | 1 | 2 | 3 | 4 | 5 |
人数 | 2 | 5 | 8 | 9 | 6 |
则这30名同学每天使用的零花钱的众数和中位数分别是( )
A.4,3
B.4,3.5
C.3.5,3.5
D.3.5,4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com