
分析 各方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.
解答 解:(1)去分母得:15x-12=4x+10-3x+6,
移项合并得:14x=28,
解得:x=2,
经检验x=2是增根,分式方程无解;
(2)去分母得:x-1+2x+2=4,
解得:x=1,
经检验x=1是增根,分式方程无解;
(3)去分母得:8-(2x+3)(2x+1)=-4x2+1,
去括号得:8-4x2-8x-3=-4x2+1,
解得:x=$\frac{1}{2}$,
经检验x=$\frac{1}{2}$是增根,分式方程无解;
(4)去分母得:6-2(x+1)=-(x-2),
去括号得:6-2x-2=-x+2,
解得:x=2,
经检验x=2是增根,分式方程无解.
点评 此题考查了解分式方程,解分式方程的基本思想是“转化思想”,把分式方程转化为整式方程求解.解分式方程一定注意要验根.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
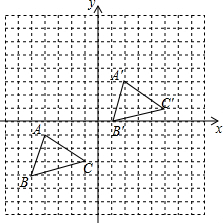 如图所示,将△ABC先向右平移6个单位长度,再向上平移4个单位长度,得到△A′B′C′,△ABC三个顶点的坐标分别为A(-4,-1)、B(-5,-4)、C(-1,-3).
如图所示,将△ABC先向右平移6个单位长度,再向上平移4个单位长度,得到△A′B′C′,△ABC三个顶点的坐标分别为A(-4,-1)、B(-5,-4)、C(-1,-3).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
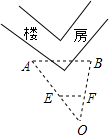 如图,为了测量有障碍物相隔的A、B两点间的距离,请你通过构造位似图形,设计一种测量方案,需要测量的数据用a,b,c,…表示,并求出A、B间的距离.
如图,为了测量有障碍物相隔的A、B两点间的距离,请你通过构造位似图形,设计一种测量方案,需要测量的数据用a,b,c,…表示,并求出A、B间的距离.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
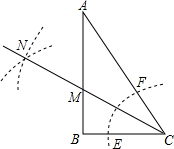 Rt△ABC中,∠B=90°∠A=30°.以C为圆心,小于BC长为半径画弧与AC、BC边交于点F、E.分别以E、F为圆心,大于$\frac{1}{2}$EF为半径画弧,两弧交于点N,若BC=$\sqrt{3}$,则点M到AC的距离是( )
Rt△ABC中,∠B=90°∠A=30°.以C为圆心,小于BC长为半径画弧与AC、BC边交于点F、E.分别以E、F为圆心,大于$\frac{1}{2}$EF为半径画弧,两弧交于点N,若BC=$\sqrt{3}$,则点M到AC的距离是( )| A. | 1 | B. | $\sqrt{3}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com