
ij�߲˾�����ȥ�߲�������������ij���߲ˣ���֪�����߲˵���������20ǧ�ˡ�60ǧ��֮�䣨��20ǧ�˺�60ǧ�ˣ�ʱ��ÿǧ����������5Ԫ��������60ǧ��ʱ�������������߲�ȫ������ۣ��������ܽ�������300Ԫ��
��1���������⣬��д�����
�߲˵���������ǧ�ˣ� �� 25 60 75 90 ��
�����Ľ�Ԫ�� �� 125 ������������ 300 ������������ ��
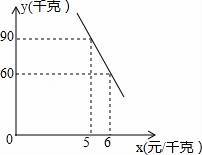
��2�������飬���߲˾��������۸����߲˵���������y��ǧ�ˣ������ۼ�x��Ԫ/ǧ�ˣ���һ�κ�����ϵ����ͼ����ͼ�����y��x֮��ĺ�����ϵʽ��
��3�������߲˾�����ÿ�����۴����߲˲�����75ǧ�ˣ��ҵ������ۼ۲��䣬��ô���ۼ۶�Ϊ����ʱ���þ��������۴����߲˵ĵ�����������������Ϊ����Ԫ��

�����㡿���κ�����Ӧ�ã�һ�κ�����Ӧ�ã�
����������1�����������߲˵���������20ǧ�ˡ�60ǧ��֮�䣨��20ǧ�˺�60ǧ�ˣ�ʱ��ÿǧ����������5Ԫ���ɵ�60��5=300Ԫ��������60ǧ��ʱ�������������߲�ȫ������ۣ���90��5��0.8=360Ԫ��
��2���ѵ㣨5��90������6��60�����뺯������ʽy=kx+b��k��0�����г������飬ͨ���ⷽ������ú�����ϵʽ��
��3�������������=y��x��4�������������䷽�����������ֵ���ɣ�
����𡿽⣺��1��������֪��
���߲�������Ϊ60ǧ��ʱ��60��5=300��Ԫ����
���߲�������Ϊ90ǧ��ʱ��90��5��0.8=360��Ԫ����
�ʴ�Ϊ��300��360��
��2�����һ�κ�������ʽΪy=kx+b��k��0�����ѵ㣨5��90������6��60�����룬��
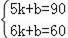
 ��
��
���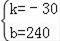
 ��
��
�ʸ�һ�κ�������ʽΪ��y=��30x+240��
��3���赱�տɻ�����w��Ԫ���������ۼ�ΪxԪ���ɣ�2��֪��
w=����30x+240����x��5��0.8��=��30��x��6��2+120����30x+240��75����x��5.5��
��x=5.5ʱ�����տɻ����������������Ϊ112.5Ԫ��
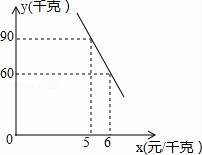

��������������Ҫ������һ�κ�����Ӧ���Լ����κ�����Ӧ�ã��ó�y��x�ĺ�����ϵʽ�ǽ���ؼ���
��


 ��������ϵ�д�
��������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
�۲�����һ���ʽ�Ļ���Ȼ�������� ���⣺
 =
= =
= ��
�� =
= =
= ��
��
 =
= =2﹣
=2﹣ ��
��
��1���ڼ��������ҳ����� =
= ﹣
﹣ ��n��ʾ����0����Ȼ����
��n��ʾ����0����Ȼ����
��2��ͨ������������̣���֪ ��
�� ���조��������������=������
���조��������������=������
��3�������㷢�ֵĹ��ɼ�������ʽ�ӵ�ֵ��
�� ��+
��+ ����
���� ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
��֪��A��m﹣1��3�����B��2��n﹣1������x��Գƣ���m+n��2015��ֵΪ( )
A��0 B��﹣1 C��1 D��32015
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
��ͼ���ڡ�ABC�У�AB=10��AC=8��BC=6��������C�����AB���еĶ�Բ��CB��CA�ֱ��ཻ�ڵ�E��F�����߶�EF���ȵ���Сֵ����������������


�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
��ͼ����һ�ŵ�������ֽƬ����λ������ƴ��һ���µ�ͼ�Σ�����µ�ͼ�ο���������ͼ���еģ�������


A�������� B��ƽ���ı��� C������ D��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
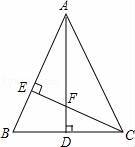
��ͼ����ABC�У�AB=AC��AD��BC��CE��AB��AE=CE����֤��
��1����AEF�ա�CEB��
��2��AF=2CD��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
ϣ����ѧѧ����2014��12�·ݿ�ʼÿ�ܺ�Ӫ��ţ�̣�����Ϊ2Ԫ/�У��ܼ�yԪ��Ӫ��ţ�̺���x�仯.ָ�����еij�����������Ա����뺯������д����ʾ�������Ա�����ϵ��ʽ��.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����A����3����2������ƽ��5����λ��������ƽ��4����λ�õ���B�����B������Ϊ��������
A������8��2�� B������8����6�� C����2����2�� D����2��2��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com