
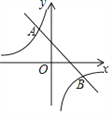
【题目】如图,一次函数y=k1x+b与反比例函数y=![]() 的图象交于点A(m,2),B(2,-1).
的图象交于点A(m,2),B(2,-1).
(1)求这两个函数的表达式;
(2)在x轴上是否存在点P(n,0),使△ABP为直角三角形,请你直接写出P点的坐标.
【答案】(1)![]() ;y=-x+1;(2)P点的坐标(3,0)、(﹣3,0)、(
;y=-x+1;(2)P点的坐标(3,0)、(﹣3,0)、(![]() ,0)或(
,0)或(![]() ,0).
,0).
【解析】分析:(1)把点B坐标代入y=![]() 求出反比例函数的解析式,再把点A坐标代入反比例函数的解析式求出m的值,利用待定系数法求出一次函数解析式.
求出反比例函数的解析式,再把点A坐标代入反比例函数的解析式求出m的值,利用待定系数法求出一次函数解析式.
(2)分三种情况进行讨论, ①当∠BAP=90°; ②当∠BPA=90°; ③当∠PBA=90°, 利用勾股定理的逆定理建立方程即可得出结论.
详解: (1)把A(1,2)代入y=![]() 得:2=k 1
得:2=k 1
∴k =2×(1)=2
∴![]()
把B(m,2)代入![]() 得:m=-1,
得:m=-1,
∴B(-1,2)
把A(1,2),B(2,1)分别代入y=k x+b得:
![]()
∴![]()
∴y=x+1
(2)∵A(1,2),B(2,1),P(n,0),
∴AB =18,AP =(n+1) +4,BP =(n2) +1,
∵△ABP为直角三角形,
∴①当∠ABP=90°时,AB +BP =AP ,
∴18+(n2) +1=(n+1) +4,
∴n=3,
∴P(3,0),
②当∠BAP=90°时,AB +AP =BP ,
∴18+(n+1) +4=(n2) +1,
∴n=3,
∴P(3,0),
③当∠APB=90°时,AP +BP =AB ,
∴(n+1) +4+(n2) +1=18,
∴n=![]() ,
,
∴P(![]() ,0)或(
,0)或(![]() ,0)
,0)
即:P点的坐标(3,0)、(3,0)、(![]() ,0)或(
,0)或(![]() ,0).
,0).
点睛: 本题考查反比例函数和一次函数解析式的确定、等腰直角三角形的判定等知识及综合应用知识、解决问题的能力.要注意在不确定直角三角形的直角边和底边的情况下要考虑到所有的情况,不要漏解.


科目:初中数学 来源: 题型:
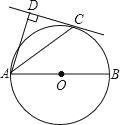
【题目】如图,AB为⊙O的直径,C为⊙O上一点,AD和过C点的切线互相垂直,垂足为D.
(1)求证:AC平分∠DAB;
(2)过点O作线段AC的垂线OE,垂足为E(要求:尺规作图,保留作图痕迹,不写作法);
(3)若CD=4,AC=4![]() ,求垂线段OE的长.
,求垂线段OE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
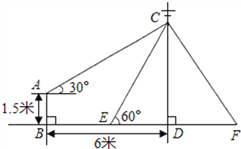
【题目】如图,在电线杆上的C处引拉线CE、CF固定电线杆,拉线CE和地面所成的角
∠CED=60°,在离电线杆6米的B处安置测角仪AB,在A处测得电线杆上C处的仰角为30°,已知测角仪高AB为1.5米,求拉线CE的长 (结果精确到0.1米,参考数据:![]() ≈1.414,
≈1.414,![]() ≈1.732).
≈1.732).
查看答案和解析>>
科目:初中数学 来源: 题型:
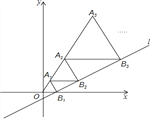
【题目】如图,在平面直角坐标系中,直线l:y=![]() x﹣
x﹣![]() 与x轴交于点B1,以OB1为边长作等边三角形A1OB1,过点A1作A1B2平行于x轴,交直线l于点B2,以A1B2为边长作等边三角形A2A1B2,过点A2作A2B3平行于x轴,交直线l于点B3,以A2B3为边长作等边三角形A3A2B3,…,则点A100的横坐标是_____.
与x轴交于点B1,以OB1为边长作等边三角形A1OB1,过点A1作A1B2平行于x轴,交直线l于点B2,以A1B2为边长作等边三角形A2A1B2,过点A2作A2B3平行于x轴,交直线l于点B3,以A2B3为边长作等边三角形A3A2B3,…,则点A100的横坐标是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
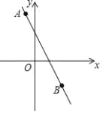
【题目】在直角坐标系中,一条直线经过A(﹣1,5),P(2,a),B(3,﹣3).
(1)求直线AB的函数表达式;
(2)求a的值;
(3)求△AOP的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,货轮O在航行过程中,发现灯塔A在它北偏东30°的方向上,海岛B在它南偏东60°方向上.则下列结论:
①∠NOA=30°;
②图中∠NOB的补角有两个,分别是∠SOB和∠EOA;
③图中有4对互余的角;
④货轮O在海岛B的西偏北30°的方向上.
其中正确结论的个数有( )

A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
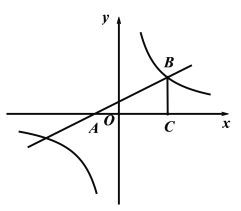
【题目】已知:如图,在平面直角坐标系xOy中,直线![]() 与x轴交于点A,在第一象限内与反比例函数图像交于点B,BC垂直于x轴,垂足为点C,且OC=2AO.求
与x轴交于点A,在第一象限内与反比例函数图像交于点B,BC垂直于x轴,垂足为点C,且OC=2AO.求
(1)点![]() 的坐标;
的坐标;
(2)反比例函数的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,□ABCD中,AB=2,BC=![]() .
.
(1)利用尺规作∠ABC的平分线BE,交AD于点E;(保留作图痕迹,不写作法)
(2)记![]() ,先化简
,先化简![]() ,再求
,再求![]() 的值.
的值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com