
【题目】如图,□ABCD中,AB=2,BC=![]() .
.
(1)利用尺规作∠ABC的平分线BE,交AD于点E;(保留作图痕迹,不写作法)
(2)记![]() ,先化简
,先化简![]() ,再求
,再求![]() 的值.
的值.

 智慧小复习系列答案
智慧小复习系列答案科目:初中数学 来源: 题型:
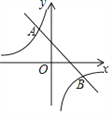
【题目】如图,一次函数y=k1x+b与反比例函数y=![]() 的图象交于点A(m,2),B(2,-1).
的图象交于点A(m,2),B(2,-1).
(1)求这两个函数的表达式;
(2)在x轴上是否存在点P(n,0),使△ABP为直角三角形,请你直接写出P点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
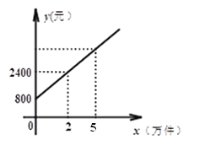
【题目】某公司市场营销部的某营销员的个人月收入与该营销员每月的销售量成一次函数关系,其图像如图所示.根据图像提供的信息,解答下列问题:
(1)求营销员的个人月收入y元与该营销员每月的销售量x万件(x≥0)之间的函数关系式;
(2)若两个月内该营销员的销售量从2万件猛增到5万件,月收入两个月大幅度增长,且连续两个月的月收入的增长率是相同的,试求这个增长率(![]() ,保留到百分位).
,保留到百分位).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市交警大队一辆警车每天在一段东西方向的公路上巡逻执法.一天上午从![]() 地出发,中午到达
地出发,中午到达![]() 地,规定向东行驶的里程为正,向西行驶的里程为负,这天行驶的里程数记录如下(单位:
地,规定向东行驶的里程为正,向西行驶的里程为负,这天行驶的里程数记录如下(单位:![]() );
);![]() ,
,
(1)问![]() 地在
地在![]() 地的东面还是西面?
地的东面还是西面?![]() ,
,![]() 两地相距多少千米?
两地相距多少千米?
(2)若该警车每千米耗油![]() 升,警车出发时,油箱中有油
升,警车出发时,油箱中有油![]() 升,请问中途有没有给警车加过油?若有,至少加了多少升油?请说明理由.
升,请问中途有没有给警车加过油?若有,至少加了多少升油?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两车分别从A、B两地同时出发,甲车匀速前往B地,到达B地立即以另一速度按原路匀速返回到A地;乙车匀速前往A地,设甲、乙两车距A地的路程为y(千米),甲车行驶的时间为x(时),y与x之间的函数图象如图所示
(1)求甲车从A地到达B地的行驶时间;
(2)求甲车返回时y与x之间的函数关系式,并写出自变量x的取值范围;
(3)求乙车到达A地时甲车距A地的路程.

查看答案和解析>>
科目:初中数学 来源: 题型:
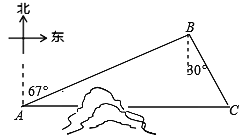
【题目】如图,C地在A地的正东方向,因有大山阻隔,由A地到C地需绕行B地,现计划开凿隧道使A、C两地直线贯通,经测量得:B地在A地的北偏东67°方向,距离A地280km,C地在B地南偏东的30°方向.
(1)求B地到直线AC的距离;
(2)求隧道开通后与隧道开通前相比,从A地到C地的路程将缩短多少?
(本题结果都精确到0.1km)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】教材在探索平方差公式时利用了面积法,面积法除了可以帮助我们记忆公式,还可以直观地推导或验证公式,俗称“无字证明”,例如,著名的赵爽弦图(如图①,其中四个直角三角形较大的直角边长都为a,较小的直角边长都为b,斜边长都为c),大正方形的面积可以表示为c2 , 也可以表示为4×![]() ab+(a-b)2由此推导出重要的勾股定理:如果直角三角形两条直角边长为a,b,斜边长为c,则a2+b2=c2 .
ab+(a-b)2由此推导出重要的勾股定理:如果直角三角形两条直角边长为a,b,斜边长为c,则a2+b2=c2 .

(1)图②为美国第二十任总统伽菲尔德的“总统证法”,请你利用图②推导勾股定理.
(2)如图③,直角△ABC中,∠ACB=90°,AC=3cm,BC=4cm,则斜边AB上的高CD的长为多少?
(3)试构造一个图形,使它的面积能够解释(a+b)(a+2b)=a2+3ab+2b2 , 画在如图4的网格中,并标出字母a、b所表示的线段.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】你喜欢玩游戏吗?现请你玩一个转盘游戏.如图所示的两上转盘中指针落在每一个数字上的机会均等,现同时自由转动甲、乙两个转盘,转盘停止后,指针各指向一个数字,用所指的两个数字作乘积.所有可能得到的不同的积分别为_______________________;数字之积为奇数的概率为______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知矩形ABCD,点E为AD上一点,BE ⊥ AC于F点.

(1)若AE=![]() AD,△AEF的面积为1时,求△ABC的面积;
AD,△AEF的面积为1时,求△ABC的面积;
(2)若AD = 4,tan∠EAF =![]() ,求AF的长;
,求AF的长;
(3)若tan∠EAF =![]() ,连接DF,证明DF=AB.
,连接DF,证明DF=AB.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com