
ЎѕМвДїЎїХэ·ЅРОOABCµД±Яі¤ОЄ2Ј¬ЖдЦРOAЎўOC·Ц±рФЪxЦбєНyЦбЙПЈ¬ИзНјўЩЛщКѕЈ¬Ц±ПЯlѕ№эAЎўCБЅµгЈ®
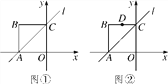
(1)ИфµгPКЗЦ±ПЯlЙПµДТ»µгЈ¬µ±ЎчOPAµДГж»эКЗ3К±Ј¬ЗлЗуіцµгPµДЧш±кЈ»
(2)ИзНјўЪЈ¬Чш±кПµxOyДЪУРТ»µгD(Ј1Ј¬2)Ј¬µгEКЗЦ±ПЯlЙПµДТ»ёц¶ЇµгЈ®
ўЩЗлЗуіц|BEЈ«DE|µДЧоРЎЦµєНґЛК±µгEµДЧш±кЈ»
ўЪИфЅ«µгDСШxЦб·ХЫµЅxЦбПВ·ЅЈ¬Ц±ЅУРґіц|BEЈDE|µДЧоґуЦµЈ¬ІўРґіцґЛК±µгEµДЧш±кЈ®
Ўѕґр°ёЎїЈЁ1Ј©P(1Ј¬3)»тP (Ј5Ј¬Ј3)Ј»ЈЁ2Ј©ўЩЧоРЎЦµОЄ![]() Ј¬E
Ј¬E![]() Ј»ўЪЧоґуЦµОЄ
Ј»ўЪЧоґуЦµОЄ![]() Ј¬µгE (2Ј¬4).
Ј¬µгE (2Ј¬4).
ЎѕЅвОцЎїЈЁ1Ј©ИзНј1ЦРЈ¬ЗуіцЦ±ПЯlµДЅвОцКЅОЄy=x+2Ј®ЙиµгPµДЧш±кОЄЈЁmЈ¬m+2Ј©Ј¬УЙМвТвµГ![]() ЎБ2ЎБ|m+2|=3Ј¬Ѕв·ЅіМјґїЙЈ»
ЎБ2ЎБ|m+2|=3Ј¬Ѕв·ЅіМјґїЙЈ»
ЈЁ2Ј©ИзНј2ЦРЈ¬Б¬ЅУODЅ»Ц±ПЯlУЪµгEЈ¬ФтµгEОЄЛщЗ󣬴ЛК±|BE+DE|=|OE+DE|=ODЈ¬ODјґОЄЧоґуЦµЈ®ЗуіцЦ±ПЯODµДЅвОцКЅЈ¬АыУГ·ЅіМЧйЗуіцµИEЧш±кјґїЙЈ»
ЈЁ3Ј©ИзНј3ЦРЈ¬OУлB№ШУЪЦ±ПЯl¶ФіЖЈ¬ЛщТФBE=OEЈ¬|BE-DE|=|OE-DE|Ј®УЙБЅ±ЯЦ®ІоРЎУЪµЪИэ±ЯЦЄЈ¬µ±µгOЈ¬DЈ¬EИэµг№ІПЯК±Ј¬|OE-DE|µДЦµЧоґуЈ¬ЧоґуЦµОЄODЈ®ЗуіцЦ±ПЯODµДЅвОцКЅЈ¬АыУГ·ЅіМЧйЗуіцЅ»µгEЧш±кјґїЙЈ®
ЅвЈє(1)ИзНјўЩЈ¬УЙМвТвЦЄµгAЎўµгCµДЧш±к·Ц±рОЄ(Ј2Ј¬0)єН(0Ј¬2)Ј®
ЙиЦ±ПЯlµДєЇКэ±нґпКЅyЈЅkxЈ«b(kЎЩ0)Ј¬
Ждѕ№эµгA(Ј2Ј¬0)єНµгC(0Ј¬2)Ј¬ґъИлµГ![]() Ј¬
Ј¬
ЅвµГ![]() Ј¬
Ј¬
ЎаЦ±ПЯlµДЅвОцКЅОЄyЈЅxЈ«2.
ЙиµгPµДЧш±кОЄ(mЈ¬mЈ«2)Ј¬УЙМвТвµГ![]() ЎБ2ЎБ|mЈ«2|ЈЅ3Ј¬
ЎБ2ЎБ|mЈ«2|ЈЅ3Ј¬
ЎаmЈЅ1»тЈ5.
ЎаP1(1Ј¬3)Ј¬P2 (Ј5Ј¬Ј3)Ј®
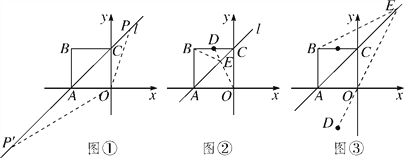
(2)ўЩИзНјўЪЈ¬Б¬ЅУODЅ»Ц±ПЯlУЪµгEЈ¬ФтµгEОЄЛщЗуЈ¬
ґЛК±|BEЈ«DE|ЈЅ|OEЈ«DE|ЈЅODЈ¬ODјґОЄЧоРЎЦµЈ®
ЙиODЛщФЪЦ±ПЯОЄyЈЅk1x(k1ЎЩ0)Ј¬ѕ№эµгD(Ј1Ј¬2)Ј¬
Ўаk1ЈЅЈ2Ј¬
ЎаЦ±ПЯODµДЅвОцКЅОЄyЈЅЈ2x.
УЙ![]() Ј¬ЅвµГ
Ј¬ЅвµГ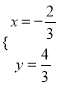 Ј¬
Ј¬
ЎаµгEµДЧш±кОЄ![]() .
.
УЦЎЯµгDµДЧш±кОЄ(Ј1Ј¬2)Ј¬
ЎаУЙ№ґ№Й¶ЁАнїЙµГODЈЅ![]() .
.
јґ|BEЈ«DE|µДЧоРЎЦµОЄ![]() .
.
ўЪИзНјўЫЈ¬ЎЯOУлB№ШУЪЦ±ПЯl¶ФіЖЈ¬
ЎаBEЈЅOEЈ¬
Ўа|BEЈDE|ЈЅ|OEЈDE|.
УЙИэЅЗРОµДБЅ±ЯЦ®ІоРЎУЪµЪИэ±ЯЦЄЈ¬µ±µгOЈ¬DЈ¬EИэµг№ІПЯК±Ј¬|OEЈDE|µДЦµЧоґуЈ¬ЧоґуЦµОЄOD.
ЎЯD(Ј1Ј¬Ј2)Ј¬
ЎаЦ±ПЯODµДЅвОцКЅОЄyЈЅ2xЈ¬ODЈЅ![]() ЈЅ
ЈЅ![]() .
.
УЙ![]() ЅвµГ
ЅвµГ![]() Ј¬
Ј¬
ЎаµгEµДЧш±кОЄ(2Ј¬4)Ј®
Ўа|BEЈDE|µДЧоґуЦµОЄ![]() Ј¬ґЛК±µгEµДЧш±кОЄ(2Ј¬4)Ј®
Ј¬ґЛК±µгEµДЧш±кОЄ(2Ј¬4)Ј®



| Дкј¶ | ёЯЦРїОіМ | Дкј¶ | іхЦРїОіМ |
| ёЯТ» | ёЯТ»Гв·СїОіМНЖјцЈЎ | іхТ» | іхТ»Гв·СїОіМНЖјцЈЎ |
| ёЯ¶ю | ёЯ¶юГв·СїОіМНЖјцЈЎ | іх¶ю | іх¶юГв·СїОіМНЖјцЈЎ |
| ёЯИэ | ёЯИэГв·СїОіМНЖјцЈЎ | іхИэ | іхИэГв·СїОіМНЖјцЈЎ |
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїИзНј1Ј¬ТСЦЄЎчBADєНЎчBCEѕщОЄµИСьЦ±ЅЗИэЅЗРОЈ¬ЎПBAD=ЎПBCE=90ЎгЈ¬µгMОЄDEµДЦРµгЈ®№эµгEУлADЖЅРРµДЦ±ПЯЅ»ЙдПЯAMУЪµгNЈ®
ЈЁ1Ј©µ±AЈ¬BЈ¬CИэµгФЪН¬Т»Ц±ПЯЙПК±ЈЁИзНј1Ј©Ј¬ЗуЦ¤ЈєMОЄANµДЦРµгЈ»
ЈЁ2Ј©Ѕ«Нј1ЦРЎчBCEИЖµгBРэЧЄЈ¬µ±AЈ¬BЈ¬EИэµгФЪН¬Т»Ц±ПЯЙПК±ЈЁИзНј2Ј©Ј¬ЗуЦ¤ЈєЎчCANОЄµИСьЦ±ЅЗИэЅЗРОЈ»
ЈЁ3Ј©Ѕ«Нј1ЦРЎчBCEИЖµгBРэЧЄµЅНј3µДО»ЦГК±Ј¬(2)ЦРµДЅбВЫКЗ·сИФИ»іЙБўЈїИфіЙБўЈ¬КФЦ¤ГчЦ®Ј»ИфІ»іЙБўЈ¬ЗлЛµГчАнУЙЈ®

Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїИзНјЛщКѕ,Ѕ«ЎчABCСШЧЕДіТ»·ЅПтЖЅТЖТ»¶ЁµДѕаАлµГµЅЎчMNL,ФтПВБРЅбВЫЦРХэИ·µДУРЈЁЎЎ Ј©
ўЩAMЎОBNЈ»ўЪAM=BNЈ»ўЫBC=MLЈ»ўЬЎПACB=ЎПMNLЎЈ

A. 1ёц B. 2ёц C. 3ёц D. 4ёц
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїИзНјЈ¬ФЪЖЅГжЦ±ЅЗЧш±кПµxOyЦРЈ¬ИэЅЗ°еµДЦ±ЅЗ¶ҐµгPµДЧш±кОЄ(2Ј¬2)Ј¬Т»МхЦ±ЅЗ±ЯУлxЦбµДХэ°лЦбЅ»УЪµгAЈ¬БнТ»Ц±ЅЗ±ЯУлyЦбЅ»УЪµгBЈ¬ИэЅЗ°еИЖµгPФЪЧш±кЖЅГжДЪЧЄ¶ЇµД№эіМЦРЈ¬µ±ЎчPOAОЄµИСьИэЅЗРОК±Ј¬ЗлРґіцЛщУРВъЧгМхјюµДµгBµДЧш±к__________Ј®
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїµ±xЈЅ1К±Ј¬ax+b+1ЈЅ©Ѓ3Ј¬ФтЈЁa+b©Ѓ1Ј©ЈЁ1©Ѓa©ЃbЈ©µДЦµОЄ_____Ј®
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїТСЦЄЈєФЪЖЅГжЦ±ЅЗЧш±кПµЦРЈ¬ЛД±ЯРОABCDКЗі¤·ЅРОЈ¬ЎПAЈЅЎПBЈЅЎПCЈЅЎПDЈЅ90ЎгЈ¬ABЎОCDЈ¬ABЈЅCDЈЅ8Ј¬ADЈЅBCЈЅ6Ј¬DµгУлФµгЦШєПЈ¬Чш±кОЄЈЁ0Ј¬0Ј©.
ЈЁ1Ј©Ц±ЅУРґіцµгBµДЧш±к__________.
ЈЁ2Ј©¶ЇµгPґУµгAіц·ўТФГїГл3ёцµҐО»і¤¶ИµДЛЩ¶ИПтЦХµгBФИЛЩФЛ¶ЇЈ¬¶ЇµгQґУµгCіц·ўТФГїГл4ёцµҐО»і¤¶ИµДЛЩ¶ИСШЙдПЯCD·ЅПтФИЛЩФЛ¶ЇЈ¬ИфPЈ¬QБЅµгН¬К±іц·ўЈ¬ЙиФЛ¶ЇК±јдОЄtГлЈ¬µ±tОЄєОЦµК±Ј¬PQЎОyЦбЈї

Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїДіЙМИЛФЪТ»ґОВтВфЦРѕщТФ120ФЄВфіцБЅјюТВ·ю,Т»јюЧ¬20ЈҐ,Т»јюЕв20ЈҐ,ФЪХвґОЅ»ТЧЦР,ёГЙМИЛЈЁ Ј©
A.Ч¬10ФЄB.Ев10ФЄC.І»Ч¬І»ЕвD.ОЮ·ЁИ·¶Ё
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
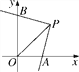
ЎѕМвДїЎїИзНјЈ¬ФЪЖЅГжЦ±ЅЗЧш±кПµЦРЈ¬№эµгBЈЁ6Ј¬0Ј©µДЦ±ПЯABУлЦ±ПЯOAПаЅ»УЪµгAЈЁ4Ј¬2Ј©Ј¬¶ЇµгMФЪПЯ¶ОOAєНЙдПЯACЙПФЛ¶ЇЈ®
ЈЁ1Ј©ЗуЦ±ПЯABµДЅвОцКЅЈ®
ЈЁ2Ј©ЗуЎчOACµДГж»эЈ®
ЈЁ3Ј©КЗ·сґжФЪµгMЈ¬К№ЎчOMCµДГж»эКЗЎчOACµДГж»эµД![]() ЈїИфґжФЪЗуіцґЛК±µгMµДЧш±кЈ»ИфІ»ґжФЪЈ¬ЛµГчАнУЙЈ®
ЈїИфґжФЪЗуіцґЛК±µгMµДЧш±кЈ»ИфІ»ґжФЪЈ¬ЛµГчАнУЙЈ®

Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїТ»¶СУРємЎў°ЧБЅЦЦСХЙ«µДЗтИфёЙёцЈ¬ТСЦЄ°ЧЗтµДёцКэ±ИємЗтЙЩЈ¬µ«°ЧЗтµД2±¶±ИємЗт¶аЈ®Иф°СГїТ»ёц°ЧЗт¶јјЗЧчЎ°2Ў±Ј¬ГїТ»ёцємЗт¶јјЗЧчЎ°3Ў±Ј¬ФтЧЬКэОЄЎ°60Ў±Ј¬ДЗГґХвБЅЦЦЗтёчУР¶аЙЩёцЈї
Ійїґґр°ёєНЅвОц>>
№ъјКѧУУЕСЎ - Б·П°ІбБР±н - КФМвБР±н
єю±±КЎ»ҐБЄНшОҐ·ЁєНІ»БјРЕПўѕЩ±ЁЖЅМЁ | НшЙПУРє¦РЕПўѕЩ±ЁЧЁЗш | µзРЕХ©ЖѕЩ±ЁЧЁЗш | ЙжАъК·РйОЮЦчТеУРє¦РЕПўѕЩ±ЁЧЁЗш | ЙжЖуЗЦИЁѕЩ±ЁЧЁЗш
ОҐ·ЁєНІ»БјРЕПўѕЩ±Ёµз»°Јє027-86699610 ѕЩ±ЁУКПдЈє58377363@163.com