
【题目】在平面直角坐标系中,已知抛物线y=ax2+bx+c(a>0)与x轴交于A(﹣1,0)、B两点(点A在点B的左侧),与y轴交于点C,抛物线的顶点为点D,对称轴为直线x=1,交x轴于点E,tan∠BDE=![]() .
.
(1)求抛物线的表达式;
(2)若点P是对称轴上一点,且∠DCP=∠BDE,求点P的坐标.
【答案】(1)y=x2﹣2x﹣3;(2)点P的坐标为(1,﹣6)或(1,﹣![]() ).
).
【解析】
(1)由点A的坐标及抛物线的对称轴可得出AE=2,利用二次函数的性质可得出BE=2,结合tan∠BDE=![]() ,可得出DE的长度,进而可得出点D的坐标,抛物线的表达式可设为y=a(x﹣1)2﹣4,根据点A的坐标,利用待定系数法可求出a的值,进而可得出抛物线的表达式;
,可得出DE的长度,进而可得出点D的坐标,抛物线的表达式可设为y=a(x﹣1)2﹣4,根据点A的坐标,利用待定系数法可求出a的值,进而可得出抛物线的表达式;
(2)取点F(5,0),连接DF,过点C作CM⊥直线DE,垂足为点M,过点B作BN⊥直线DF,垂足为点N,则△DEF,△BNF为等腰直角三角形,根据等腰直角三角形的性质可求出BN,DN的长度,进而可得出tan∠BDN=![]() ,利用二次函数图象上点的坐标特征可得出点C的坐标,结合点D的坐标可得出△CDM为等腰直角三角形,分点P在点D的下方和点P在点D的上方两种情况考虑:①当点P在点D下方时,由∠CDM=∠DCP+∠CPM=45°,∠BDE+∠BDN=45°可得出∠CPM=∠BDN,进而可得出tan∠CPM=
,利用二次函数图象上点的坐标特征可得出点C的坐标,结合点D的坐标可得出△CDM为等腰直角三角形,分点P在点D的下方和点P在点D的上方两种情况考虑:①当点P在点D下方时,由∠CDM=∠DCP+∠CPM=45°,∠BDE+∠BDN=45°可得出∠CPM=∠BDN,进而可得出tan∠CPM=![]() =
=![]() ,代入CM=1可求出MP,进而可求出点P的坐标;②当点P在点D上方时,由∠PCD+∠PCM=45°,∠BDE+∠BDN=45°可得出∠PCM=∠BDN,进而可得出tan∠PCM=
,代入CM=1可求出MP,进而可求出点P的坐标;②当点P在点D上方时,由∠PCD+∠PCM=45°,∠BDE+∠BDN=45°可得出∠PCM=∠BDN,进而可得出tan∠PCM=![]() =
=![]() ,代入CM=1可求出MP,进而可求出点P的坐标.综上,此题得解.
,代入CM=1可求出MP,进而可求出点P的坐标.综上,此题得解.
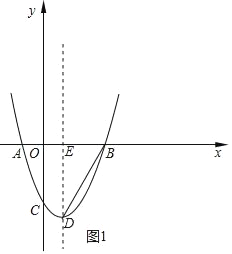
(1)依照题意,画出图形,如图1所示.
∵点A的坐标为(﹣1,0),抛物线的对称轴为直线x=1,
∴点E的坐标为(1,0),
∴BE=AE=2.
∵tan∠BDE=![]() =
=![]() ,
,
∴DE=2BE=4,
∴点D的坐标为(1,﹣4).
∴抛物线的表达式可设为y=a(x﹣1)2﹣4.
将(﹣1,0)代入y=a(x﹣1)2+4,得:4a﹣4=0,
解得:a=1,
∴抛物线的表达式为y=(x﹣1)2﹣4,即y=x2﹣2x﹣3.
(2)取点F(5,0),连接DF,过点C作CM⊥直线DE,垂足为点M,过点B作BN⊥直线DF,垂足为点N,如图2所示.
∵点D的坐标为(1,﹣4),
∴EF=DE=4,
∴△DEF为等腰直角三角形,
∴∠EDF=∠EFD=45°,DF=4![]() .
.
∵BN⊥DF,
∴△BNF为等腰直角三角形,
∴NB=NF=![]() BF=
BF=![]() ,
,
∴DN=DF﹣NF=3![]() ,
,
∴tan∠BDN=![]() =
=![]() .
.
当x=0时,y=x2﹣2x﹣3=﹣3,
∴点C的坐标为(0,﹣3).
∵点D的坐标为(1,﹣4),CM⊥DE,
∴CM=DM=1,
∴△CDM为等腰直角三角形,
∴∠DCM=∠CDM=45°.
①当点P在点D下方时,∵∠CDM=∠DCP+∠CPM=45°,∠BDE+∠BDN=45°,
∴∠CPM=∠BDN,
∴tan∠CPM=![]() =
=![]() ,即
,即![]() =
=![]() ,
,
∴MP=3,
∴EP=EM+MP=6,
∴点P的坐标为(1,﹣6);
②当点P在点D上方时,∵∠PCD+∠PCM=45°,∠BDE+∠BDN=45°,
∴∠PCM=∠BDN,
∴tan∠PCM=![]() =
=![]() ,
,
∴MP=![]() ,
,
∴EP=EM+MP=![]() ,
,
∴点P的坐标为(1,﹣![]() ).
).
综上所述,点P的坐标为(1,﹣6)或(1,﹣![]() ).
).


科目:初中数学 来源: 题型:
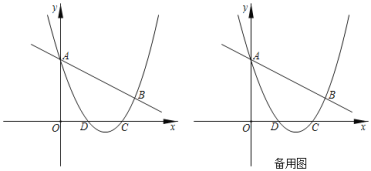
【题目】如图,抛物线![]() 与直线
与直线![]() 交于A,B两点,交x轴于D,C两点,已知
交于A,B两点,交x轴于D,C两点,已知![]() ,
,![]() .
.
![]() 求抛物线的函数表达式并写出抛物线的对称轴;
求抛物线的函数表达式并写出抛物线的对称轴;
![]() 在直线AB下方的抛物线上是否存在一点E,使得
在直线AB下方的抛物线上是否存在一点E,使得![]() 的面积最大?如果存在,求出E点坐标;如果不存在,请说明理由.
的面积最大?如果存在,求出E点坐标;如果不存在,请说明理由.
![]() 为抛物线上一动点,连接PA,过点P作
为抛物线上一动点,连接PA,过点P作![]() 交y轴于点Q,问:是否存在点P,使得以A、P、Q为顶点的三角形与
交y轴于点Q,问:是否存在点P,使得以A、P、Q为顶点的三角形与![]() 相似?若存在,请直接写出所有符合条件的P点的坐标;若不存在,请说明理由.
相似?若存在,请直接写出所有符合条件的P点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a,b,c为常数,且a≠0)中的x与y的部分对应值如下表给出了以下结论:
x | … | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | 4 | 5 | … |
y | … | 12 | 5 | 0 | ﹣3 | ﹣4 | ﹣3 | 0 | 5 | 12 | … |
①二次函数y=ax2+bx+c有最小值,最小值为﹣3;②当﹣![]() <x<2时,y<0;③二次函数y=ax2+bx+c的图象与x轴有两个交点,且它们分别在y轴的两侧;④当x<1时,y随x的增大而减小.则其中正确结论有( )
<x<2时,y<0;③二次函数y=ax2+bx+c的图象与x轴有两个交点,且它们分别在y轴的两侧;④当x<1时,y随x的增大而减小.则其中正确结论有( )
A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,∠ACB=90°,D是边AB的中点,P是边AC上一动点,BP与CD相交于点E.
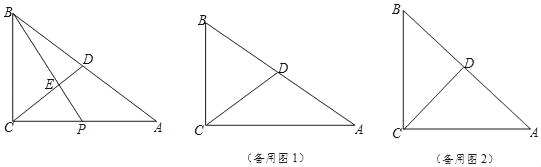
(1)如果BC=6,AC=8,且P为AC的中点,求线段BE的长;
(2)联结PD,如果PD⊥AB,且CE=2,ED=3,求cosA的值;
(3)联结PD,如果BP2=2CD2,且CE=2,ED=3,求线段PD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
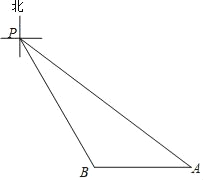
【题目】如图,P点是某海域内的一座灯塔的位置,船A停泊在灯塔P的南偏东53°方向的50海里处,船B位于船A的正西方向且与灯塔P相距20![]() 海里.(本题参考数据sin53°≈0.80,cos53°≈0.60,tan53°≈1.33.)
海里.(本题参考数据sin53°≈0.80,cos53°≈0.60,tan53°≈1.33.)
(1)试问船B在灯塔P的什么方向?
(2)求两船相距多少海里?(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
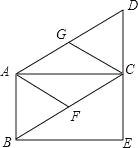
【题目】如图,在ABCD中,AC⊥CD.
(1)延长DC到E,使CE=CD,连接BE,求证:四边形ABEC是矩形;
(2)若点F,G分别是BC,AD的中点,连接AF,CG,试判断四边形AFCG是什么特殊的四边形?并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一个腰长为4cm,底边长为3cm的等腰三角形,现在要利用这个等腰三角形加工出一个边长比是1:2的平行四边形,使平行四边形的一个内角恰好是这个等腰三角形的底角,平行四边形的其他顶点均在三角形的边上,则这个平行四边形的较短的边长是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
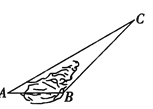
【题目】如图,A,B两地之间有一座山,汽车原来从A地到B地需经C地沿折线ACB行驶,现开通隧道后,汽车直接沿直线AB行驶即可到达B地.已知AC=120km,∠A=30°,∠B=135°,求隧道开通后汽车从A地到B地需行驶多少千米.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com