
【题目】如图,在ABCD中,AC⊥CD.
(1)延长DC到E,使CE=CD,连接BE,求证:四边形ABEC是矩形;
(2)若点F,G分别是BC,AD的中点,连接AF,CG,试判断四边形AFCG是什么特殊的四边形?并证明你的结论.
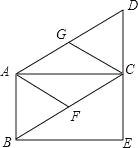
【答案】(1)证明见解析;(2)四边形AFCG是菱形.
【解析】
(1)根据矩形的判定方法,通过条件先判定四边形ABEC是平行四边形,再由AC⊥CD,得到平行四边形的一个内角是直角,可证明四边形ABEC是矩形;
(2)由中点G、F和ABCD,可证明四边形AFCG也是平行四边形,在Rt△ACD中用斜边中线等于斜边一半可得到AG=CG,进而可求证四边形AFCG是菱形.
(1)证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∵CD=CE,
∴CE∥AB,CE=AB,
∴四边形ABEC是平行四边形,
∵AC⊥CD,
∴∠ACE=90°,
∴四边形ABEC是矩形;
(2)四边形AFCG是菱形,
证明:∵四边形ABCD是平行四边形,
∴AD=CB,AD∥CB,
∵点F、G分别是BC、AD的中点,
∴AG=DG=![]() AD,BF=CF=
AD,BF=CF=![]() BC,
BC,
∴AG=CF,
∴四边形AFCG是平行四边形,
∵∠ACD=90°,G为AD的中点,
∴AG=CG,
∴四边形AFCG是菱形.


科目:初中数学 来源: 题型:
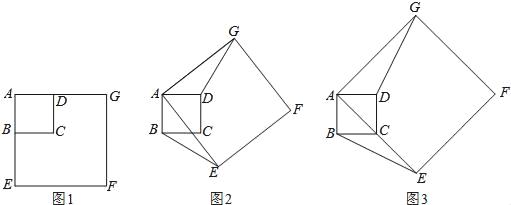
【题目】如图1,正方形ABCD与正方形AEFG的边AB、AE(AB<AE)在一条直线上,正方形AEFG以点A为旋转中心逆时针旋转,设旋转角为α.在旋转过程中,两个正方形只有点A重合,其它顶点均不重合,连接BE、DG.(1)当正方形AEFG旋转至如图2所示的位置时,求证:BE=DG;(2)如图3,如果α=45°,AB=2,AE=4![]() ,求点G到BE的距离.
,求点G到BE的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
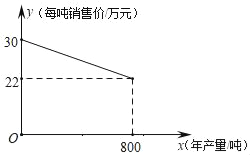
【题目】已知京润生物制品厂生产某种产品的年产量不超过800吨,生产该产品每吨所需相关费为10万元,且生产出的产品都能在当年销售完.产品每吨售价y(万元)与年产量x(吨)之间的函数关系如图所示
(1)当该产品年产量为多少吨时,当年可获得7500万元毛利润?(毛利润=销售额﹣相关费用)
(2)当该产品年产量为多少吨时,该厂能获得当年销售的是大毛利润?最大毛利润多少万元.
查看答案和解析>>
科目:初中数学 来源: 题型:
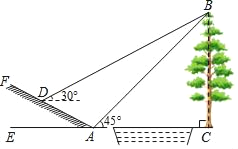
【题目】如图所示,某数学活动小组选定测量小河对岸大树BC的高度,他们在斜坡AF上的D处测得大树顶端B的仰角是30°,在地面上A处测得大树顶端B的仰角是45°.若坡角∠FAE=30°,AD=6m,求大树的高度.(结果保留整数,参考数据:![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知抛物线y=ax2+bx+c(a>0)与x轴交于A(﹣1,0)、B两点(点A在点B的左侧),与y轴交于点C,抛物线的顶点为点D,对称轴为直线x=1,交x轴于点E,tan∠BDE=![]() .
.
(1)求抛物线的表达式;
(2)若点P是对称轴上一点,且∠DCP=∠BDE,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
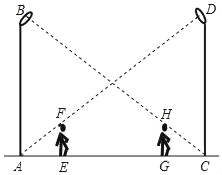
【题目】如图,为了测量两个路灯之间的距离,小明在夜晚由路灯AB走向路灯CD,当他走到点E时,发现身后他头顶部F的影子刚好接触到路灯AB的底部A处,当他向前再步行15m到达G点时,发现身前他头顶部H的影子刚好接触到路灯CD的底部C处,已知小明同学的身高是1.7m,两个路灯的高度都是8.5米,则AC=_____m.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】即墨素有“中国针织名城”的美誉,2016年,又被中国服装协会授予“中国童装名称”的称号,该区一网店销售某款童装,当每件售价80元时,每周可卖200件,为了促销,该网店决定降价销售.市场调查反映:每降价1元,每星期可多卖20件.已知该款童装每件成本价60元,设该款童装每件售价x(60≤x≤80)元,每周的销售量为y件.
(1)求y与x之间的函数关系式;
(2)设每周的销售利润为W元,当每件售价定为多少元时,每周的销售利润最大,最大利润多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
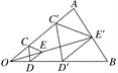
【题目】如图,用下面的方法可以画△AOB的内接等边三角形,阅读后解答相应问题.
画法:①在△AOB内画等边三角形CDE,使点C在OA上,点D在OB上;②连接OE并延长,交AB于点E′,过点E′作E′C′∥EC,交OA于点C′,作E′D′∥ED,交OB于点D′;③连接C′D′,则△C′D′E′是△AOB的内接等边三角形.
(1)求证:△C′D′E′是等边三角形;
(2)求作:内接于已知△ABC的矩形DEFG,使它的边EF在BC上,顶点D,G分别在AB,AC上,且DE:EF=1∶2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知双曲线![]() ,经过点D(6,1),点C是双曲线第三象限上的动点,过C作CA⊥x轴,过D作DB⊥y轴,垂足分别为A,B,连接AB,BC.
,经过点D(6,1),点C是双曲线第三象限上的动点,过C作CA⊥x轴,过D作DB⊥y轴,垂足分别为A,B,连接AB,BC.
(1)求k的值;
(2)若△BCD的面积为12,求直线CD的解析式;
(3)判断AB与CD的位置关系,并说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com