解:(1)令y
1=0,则x=3,
∴A点坐标是(3,0);
(2)∵∠BCO与∠BAO互为补,
∴∠BCO+∠BAO=180°,
∵四边形ABCO的内角和等于360°,∠O=90°,
∴∠ABC=90°,
∴AB⊥BC;
(3)设B点坐标是(c,d),过B分别向x、y轴做垂线段,交点分别F、E,
∵∠BCO与∠BAO互为补角,
∴∠BCO+∠BAO=180°,
∵∠BAO+∠BAF=180°,
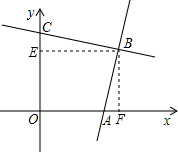
∴∠BCE=∠BAF,
在△BCE和△BAF中,
∵
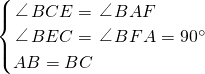
,
∴△BCE≌△BAF,
∴BF=BE,CE=AF,
∴c=d,b-c=c-3,
∵S
△BCO=7,
∴

cb=7,b=2c-3,
解得
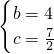
或
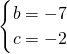
(不合题意,舍去)
故B点坐标是(

,

),
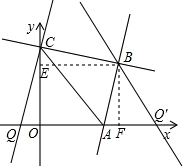
那么过B点的反比例函数的解析式是y=
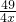
(x>0);
(4)如右图,过点C作CQ∥AB,交x轴于点Q,
∵直线y
1=mx-3m过B点,
∴y
1=7x-21,
∵CQ∥AB,
∴过C、Q的直线可设为y=7x+f,
∵C点坐标是(0,4),
∴过C、Q的直线是y=7x+4,
令y=0,则x=-

,
∴Q点的坐标是(-

,0).
过点B作BQ′∥AC,交x轴于Q′,
∵直线AC过A、C,
∴直线AC的解析式是y=-

x+4,
∵BQ′∥AC,
∴直线BQ′的解析式可设为y=-

x+b,
把(

,

)代入y=-

x+b中,得
b=

,
故直线BQ′的解析式是y=-

x+

,
令y=0,则x=

,
故Q′的坐标是(

,0).
∴所求Q的坐标是(-

,0)或(

,0).
分析:(1)令y
1=0,易求x=3,从而可得点A的坐标;
(2)由于∠BCO与∠BAO互为补角,四边形ABCO的内角和等于360°,∠O=90°,易求∠ABC=90°,故位置关系为垂直;
(3)先设B点坐标是(c,d),过B分别向x、y轴做垂线段,交点分别F、E,∠BCO与∠BAO互为补角,易得∠BCE=∠BAF,利用AAS可证△BCE≌△BAF,那么BF=BE,CE=AF,于是c=d,b-c=c-3①,再结合S
△BCO=7=

bc②,①②可得关于b、c的方程组,解可求b、c的值,进而可求B点坐标,易求过B点的反比例函数解析式;
(4)B点坐标已求,进而可求y
1的函数解析式,由(3)也可知道C点的坐标,过点C作CQ∥AB,交x轴于点Q,过C、Q的直线平行于直线AB,且与y轴交于点C,从而易求过C、Q的直线的解析式,令y=0,可求x=-

,这就是Q点的坐标.
点评:本题是一次函数综合题,解题的关键是利用AAS证明△BCE≌△BAF,求出点B的坐标.

 已知:如图,直线y1=mx-3m与x轴交于点A,直线y2=kx+b与y轴交于点C,两直线交于点B.
已知:如图,直线y1=mx-3m与x轴交于点A,直线y2=kx+b与y轴交于点C,两直线交于点B.
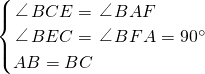 ,
, cb=7,b=2c-3,
cb=7,b=2c-3,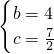 或
或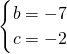 (不合题意,舍去)
(不合题意,舍去) ,
, ),
), (x>0);
(x>0);
 ,
, ,0).
,0). x+4,
x+4, x+b,
x+b, ,
, )代入y=-
)代入y=- x+b中,得
x+b中,得 ,
, x+
x+ ,
, ,
, ,0).
,0). ,0)或(
,0)或( ,0).
,0). bc②,①②可得关于b、c的方程组,解可求b、c的值,进而可求B点坐标,易求过B点的反比例函数解析式;
bc②,①②可得关于b、c的方程组,解可求b、c的值,进而可求B点坐标,易求过B点的反比例函数解析式; ,这就是Q点的坐标.
,这就是Q点的坐标.

 阅读快车系列答案
阅读快车系列答案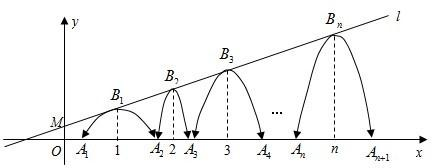
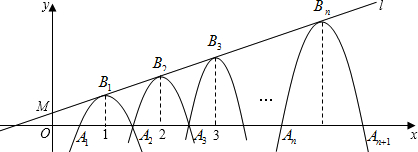
 已知:如图,一次函数y1=kx+b(k≠0)的图象与反比例函数y2=
已知:如图,一次函数y1=kx+b(k≠0)的图象与反比例函数y2=