
【题目】如图,小俊在A处利用高为1.5米的测角仪AB测得楼EF顶部E的仰角为30°,然后前进12米到达C处,又测得楼顶E的仰角为60°,求楼EF的高度.(结果精确到0.1米)
【答案】解:设楼EF的高为x米,可得EG=EF﹣GF=(x﹣1.5)米,
依题意得:EF⊥AF,DC⊥AF,BA⊥AF,BD⊥EF(设垂足为G),
在Rt△EGD中,DG=![]() (x﹣1.5)米,在Rt△EGB中,BG=
(x﹣1.5)米,在Rt△EGB中,BG=![]() (x﹣1.5)米,
(x﹣1.5)米,
∴CA=DB=BG﹣DG=![]() (x﹣1.5)米,
(x﹣1.5)米,
∵CA=12米,∴![]() (x﹣1.5)=12,
(x﹣1.5)=12,
解得:x=6![]() +1.5≈11.9,
+1.5≈11.9,
则楼EF的高度约为11.9米.
【解析】设楼EF的高为x米,由EG=EF﹣GF表示出EG,根据题意得到EF与AF垂直,DC与AF垂直,BA与AF垂直,BD与EF垂直,在直角三角形EGD中,利用锐角三角函数定义表示出DG,在直角三角形EGB中,利用锐角三角函数定义表示出BG,根据BG﹣DG表示出DB,即为CA,根据CA的长列出关于x的方程,求出方程的解即可得到结果.


 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案科目:初中数学 来源: 题型:
【题目】顶点为(﹣ ![]() ,﹣
,﹣ ![]() )的抛物线与y轴交于点A(0,﹣4),E(0,b)(b>﹣4)为y轴上一动点,过点E的直线y=x+b与抛物线交于B、C两点.
)的抛物线与y轴交于点A(0,﹣4),E(0,b)(b>﹣4)为y轴上一动点,过点E的直线y=x+b与抛物线交于B、C两点.
(1)求抛物线的解析式;
(2)①如图1,当b=0时,求证:E是线段BC的中点;
②当b≠0时,E还是线段BC的中点吗?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=﹣x2+2x+m.
(1)如果二次函数的图像与x轴有两个交点,求m的取值范围;
(2)如图,二次函数的图像过点A(3,0),与y轴交于点B,求直线AB与这个二次函数的解析式;
(3)在直线AB上方的抛物线上有一动点D,当D与直线AB的距离DE最大时,求点D的坐标,并求DE最大距离是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,C为线段AB上一点,分别以AC、BC为边在AB的同侧作等边△HAC与等边△DCB,连接DH. 
(1)如图1,当∠DHC=90°时,求 ![]() 的值;
的值;
(2)在(1)的条件下,作点C关于直线DH的对称点E,连接AE、BE,求证:CE平分∠AEB;
(3)现将图1中△DCB绕点C顺时针旋转一定角度α(0°<α<90°),如图2,点C关于直线DH的对称点为E,则(2)中的结论是否成立并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设点Q到图形W上每一个点的距离的最小值称为点Q到图形W的距离.例如正方形ABCD满足A(1,0),B(2,0),C(2,1),D(1,1),那么点O(0,0)到正方形ABCD的距离为1. 
(1)如果⊙P是以(3,4)为圆心,1为半径的圆,那么点O(0,0)到⊙P的距离为;
(2)求点M(3,0)到直线y=2x+1的距离;
(3)如果点N(0,a)到直线y=2x+1的距离为3,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】赵爽弦图是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形,如图所示,若这四个全等直角三角形的两条直角边分别平行于x轴和y轴,大正方形的顶点B1、C1、C2、C3、…、Cn在直线y=﹣ ![]() x+
x+ ![]() 上,顶点D1、D2、D3、…、Dn在x轴上,则第n个阴影小正方形的面积为 .
上,顶点D1、D2、D3、…、Dn在x轴上,则第n个阴影小正方形的面积为 . 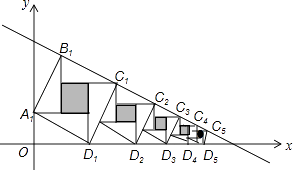
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有四张背面完全相同的卡片A,B,C,D,小伟将这四张卡片背面朝上洗匀后摸出一张,放回洗匀后再摸一张. 
(1)用树状图(或列表法)表示两次摸出卡片所有可能出现的结果(卡片可用A,B,C,D表示);
(2)求摸出两张卡片所表示的几何图形是轴对称图形而不是中心对称图形的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=ax+1与x轴、y轴分别相交于A、B两点,与双曲线y= ![]() (x>0)相交于点P,PC⊥x轴于点C,且PC=2,点A的坐标为(﹣2,0).
(x>0)相交于点P,PC⊥x轴于点C,且PC=2,点A的坐标为(﹣2,0).
(1)求双曲线的解析式;
(2)若点Q为双曲线上点P右侧的一点,且QH⊥x轴于H,当以点Q、C、H为顶点的三角形与△AOB相似时,求点Q的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com