
【题目】如图,△ABC中,D是BC的中点,过D点的直线GF交AC于F,交AC的平行线BG于G点,DE⊥DF,交AB于点E,连结EG、EF.

(1)求证:BG=CF.
(2)请你判断BE+CF与EF的大小关系,并说明理由.
【答案】(1)证明见解析;(2)BE+CF>EF.理由见解析.
【解析】试题分析:(1)先利用ASA判定△BGD≌△CFD,从而得出BG=CF;
(2)再利用全等的性质可得GD=FD,再有DE⊥GF,从而得出EG=EF,两边和大于第三边从而得出BE+CF>EF.
试题解析:(1)∵BG∥AC,
∴∠DBG=∠DCF.
∵D为BC的中点,
∴BD=CD
又∵∠BDG=∠CDF,
在△BGD与△CFD中,
∵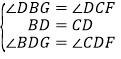
∴△BGD≌△CFD(ASA).
∴BG=CF.
(2)BE+CF>EF.
∵△BGD≌△CFD,
∴GD=FD,BG=CF.
又∵DE⊥FG,
∴EG=EF(垂直平分线到线段端点的距离相等).
∴在△EBG中,BE+BG>EG,
即BE+CF>EF.


 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案科目:初中数学 来源: 题型:
【题目】已知锐角三角形ABC内接于⊙O,AD⊥BC,垂足为D.
(1)如图1, ![]() ,BD=DC,求∠B的度数;
,BD=DC,求∠B的度数;
(2)如图2,BE⊥AC,垂足为E,BE交AD于点F,过点B作BG∥AD交⊙O于点G,在AB边上取一点H,使得AH=BG.求证:△AFH是等腰三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知∠MAN=120°,点C是∠MAN的平分线AQ上的一个定点,点B,D分别在AN,AM上,连接BD.
【发现】
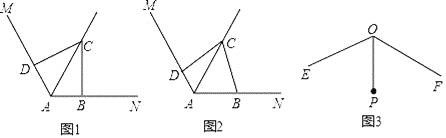
(1)如图1,若∠ABC=∠ADC=90°,则∠BCD= °,△CBD是 三角形;
【探索】
(2)如图2,若∠ABC+∠ADC=180°,请判断△CBD的形状,并证明你的结论;
【应用】
(3)如图3,已知∠EOF=120°,OP平分∠EOF,且OP=1,若点G,H分别在射线OE,OF上,且△PGH为等边三角形,则满足上述条件的△PGH的个数一共有 .(只填序号)
①2个②3个③4个④4个以上
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为深化义务教育课程改革,某校积极开展拓展性课程建设,设计开设艺术、体育、劳技、文学等多个类别的拓展性课程,要求每一位学生都自主选择一个类别的拓展性课程。为了了解学生选择拓展性课程的情况,随机抽取了部分学生进行调查,并将调查结果绘制成如下统计图(部分信息未给出):

根据统计图中的信息,解答下列问题:
(1)求本次被调查的学生人数;
(2)将条形图补充完整;
(3)若该校共有1600名学生,请估计全校选择体育类的学生人数。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解九年级学生的体能情况,随机抽取部分男生进行引体向上测试,并根据抽测成绩绘制成如下两幅统计图.


(![]() )本次抽测的学生总人数为__________;请你补全图
)本次抽测的学生总人数为__________;请你补全图![]() 的统计图.
的统计图.
(![]() )本次抽测成绩的众数为__________次;中位数为__________次.
)本次抽测成绩的众数为__________次;中位数为__________次.
(![]() )若规定引体向上
)若规定引体向上![]() 次以上(含
次以上(含![]() 次)为体能达到优秀,则该校
次)为体能达到优秀,则该校![]() 名九年级男生中,估计有多少人能达到优秀?
名九年级男生中,估计有多少人能达到优秀?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如右图,在每个小正方形边长为1的方格纸中,△ABC的顶点都在方格纸格点上.将△ABC向左平移2格,再向上平移4格.
(1)请在图中画出平移后的△ABC,
(2)再在图中画出△ABC的高CD,
(3)在右图中能使S△ABC=S△PBC的格点P的个数有 个(点P异于A)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,若干个全等的正五边形排成环状,图中所示的是前3个正五边形,要完成这一圆环还需正五边形的个数为( )

A. 10 B. 9 C. 8 D. 7
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地区为绿化环境,计划购买甲、乙两种树苗共计n棵.有关甲、乙两种树苗的信息如图所示:

(1)当n=400时,如果购买甲、乙两种树苗共用27000元,那么甲、乙两种树苗各买了多少棵?
(2)实际购买这两种树苗的总费用恰好为27000元,其中甲种树苗买了m棵.
①写出m与n满足的关系式;
②要使这批树苗的成活率不低于92%,求n的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com