练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    2．sin60°=（　　）
    A．$\frac{1}{2}$B．$\frac{\sqrt{2}}{2}$C．1D．$\frac{\sqrt{3}}{2}$

    分析 原式利用特殊角的三角函数值解得即可得到结果．

    解答 解：sin60°=$\frac{\sqrt{3}}{2}$，
    故选D

    点评 此题考查了特殊角的三角函数值，牢记特殊角的三角函数值是解本题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

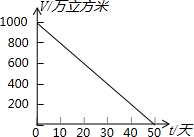    12．2007年的夏天，湖南省由于持续高温和连日无雨，水库蓄水量普遍下降，如图是某水库的蓄水量V（万立方米）与干旱持续时间t（天）之间的关系图，请根据此图，回答下列问题：
    （1）该水库原蓄水量为多少万立方米？持续干旱10天后，水库蓄水量为多少万立方米？
    （2）若水库的蓄水量小于400万立方米时，将发出严重干旱警报，请问持续干旱多少天后，将发出严重干旱警报？
    （3）按此规律，持续干旱多少天时，水库将干涸？

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

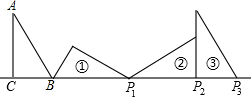    13．如图，Rt△ABC中，∠ACB=90°，AC=1，∠A=30°，且BC边在直线a上，将△ABC绕点B顺时针旋转到位置①可得到点P1，此时BP1=2；将位置①的三角形绕点P1顺时针旋转到位置②，可得到点P2，此时BP2=2+$\sqrt{3}$；将位置②的三角形绕点P2顺时针旋转到位置③，可得到点P3，此时BP3=3+$\sqrt{3}$；…，按此规律继续旋转，直至得到点P2015为止．则BP2015=2015+672$\sqrt{3}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    10．如图，在平面直角坐标系中，点O为坐标原点，直线y=kx+1（k≠0）与x轴交于点A，与y轴交于点C，过点C的抛物线y=ax2-（6a-2）x+b（a≠0）与直线AC交于另一点B，点B坐标为（4，3）．
    （1）求a的值；
    （2）点P是射线CB上的一个动点，过点P作PQ⊥x轴，垂足为点Q，在x轴上点Q的右侧取点M，使MQ=$\frac{5}{8}$，在QP的延长线上取点N，连接PM，AN，已知tan∠NAQ-tan∠MPQ=$\frac{1}{2}$，求线段PN的长；
    （3）在（2）的条件下，过点C作CD⊥AB，使点D在直线AB下方，且CD=AC，连接PD，NC，当以PN，PD，NC的长为三边长构成的三角形面积是$\frac{25}{8}$时，在y轴左侧的抛物线上是否存在点E，连接NE，PE，使得△ENP与以PN，PD，NC的长为三边长的三角形全等？若存在，求出E点坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    17．将两筐苹果分给甲、乙两班，甲班有一人分6个，其余的每人分13个；乙班有一人分5个，其余的每人分10个，并且苹果总数大于100而不超过200个，求苹果个数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    7．在⊙O中，圆心O到弦AB的距离为AB长度的一半，则弦AB所对圆心角的大小为（　　）
    A．30°B．45°C．60°D．90°

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    14．方程3（x-5）2=2（x-5）的根是x1=5，x2=$\frac{17}{3}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

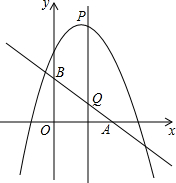    11．如图，已知直线y=-$\frac{3}{4}$x+3分别交x轴、y轴于点A、B，P是抛物线y=-$\frac{1}{2}$x2+2x+5的一个动点，其横坐标为a，过点P且平行于y轴的直线交直线y=-$\frac{3}{4}$x+3于点Q，则当PQ=BQ时，a的值是-1，4，4+2$\sqrt{5}$，4-2$\sqrt{5}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

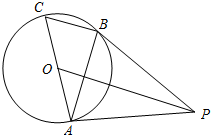    12．如图，AC是⊙O的直径，BC是⊙O的弦，点P是⊙O外一点，连接PB、AB，∠PBA=∠C．
    （1）求证：PB是⊙O的切线；
    （2）连接OP，若OP∥BC，且OP=8，⊙O的半径为2$\sqrt{2}$，求BC的长．

    查看答案和解析>>

    同步练习册答案