

分析 (1)先利用锐角三角函数求出tan∠CBD=$\frac{CD}{BC}$=$\frac{3}{4}$,即可得出PQ,再用勾股定理即可求出BQ;
(2)由(1)知MN=MQ=4t,利用锐角三角函数和勾股定理求出MH,最后用t表示三角形的面积,即可建立方程求解即可得出t值;
(3)分两种情况讨论计算,①先判断出点C,M,N在同一条直线上,得出MQ∥BD,进而得出比例式建立方程求解即可;
②判断出出点M只能在CD上,得出只有△DMN∽△MQC,即得出比例式建立方程求解即可.
解答 解:(1)如图1,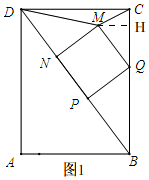 在矩形ABCD中,∠BCD=90°,CD=AB=6,BC=AD=8,
在矩形ABCD中,∠BCD=90°,CD=AB=6,BC=AD=8,
∴BD=10,
在Rt△BCD中,tan∠CBD=$\frac{CD}{BC}$=$\frac{3}{4}$,
∵四边形PQMN是正方形,
∴PQ=QM=MN=PN,∠DNM=∠PQM=∠BPQ=90°,
在Rt△BPQ中,PB=4t,
∴tan∠CBD=$\frac{PQ}{PB}$=$\frac{3}{4}$,
∴$\frac{PQ}{4t}=\frac{3}{4}$,
∴PQ=3t,
∴QM=MN=PN=PQ=3t,
根据勾股定理得,BQ=$\sqrt{P{B}^{2}+P{Q}^{2}}$=5t,
(2)①点N在BD上,由(1)知,∠PBQ+∠PQB=90°,∠CQM+∠PQB=90°,
∴∠PBQ=∠CQM,
过点M作MH⊥BC于H,
在Rt△MHQ中,tan∠MQH=tan∠PBQ=$\frac{MH}{HQ}=\frac{3}{4}$,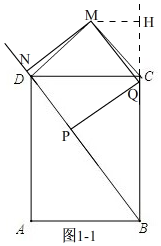
∵QM=3t,
∴MH=$\frac{3}{5}×3t$=$\frac{9}{5}$t,
∵CQ=BC-BQ=8-5t,DN=BD-PB-PN=10-7t,
∴S△CMQ=$\frac{1}{2}$CQ×MH=$\frac{1}{2}$×(8-5t)×$\frac{9}{5}$t=$\frac{9}{10}$t(8-5t),
S△DMN=$\frac{1}{2}$DN×MN=$\frac{1}{2}$×(10-7t)×3t=$\frac{3}{2}$t(10-7t)
∵△DMN与△CMQ的面积之比为5:3,
∴$\frac{\frac{3}{2}t(10-7t)}{\frac{9}{10}t(8-5t)}$=$\frac{5}{3}$,
∴t=1.
②当点N在BD延长线上时,如图1-1,
同①的方法得,t=$\frac{3}{2}$(只把①中的DN换成7t-10)
(3)存在,
如图2, ∵∠PBQ+∠BDC=90°,∠CQM=∠PBQ,
∵∠PBQ+∠BDC=90°,∠CQM=∠PBQ,
∴∠CQM+∠BDC=90°,
∵∠CQM+∠MCQ=90°,
∴∠MCQ=∠BDC,
∵△CMQ与△DMN相似,且∠DNM=90°,
∴∠CMQ=90°或∠MCQ=90°,
①当∠CMQ=90°时,
∵∠NMQ=90°,
∴点C,M,N在同一条直线上,
∵∠CNP=∠CMQ=90°,∴△DMN∽△QCM,∴$\frac{DN}{MQ}=\frac{MN}{CM}$
∵MQ=MN=3t,BN=7t,CM=$\frac{9}{4}$t,DN=10-7t
∴$\frac{10-7t}{3t}=\frac{3t}{\frac{9}{4}t}$,
∴t=$\frac{10}{11}$,
②当∠MCQ=90°时,点M在CD上,如图3,
∵∠QMN=90°,
∴∠DMN+∠CMQ=90°,
∵∠CMQ+∠CQM=90°,
∴∠DMN=∠CMQ,
∴只有△DMN∽△MQC,
∴$\frac{DN}{MN}=\frac{CM}{CQ}$,
∵$\frac{CM}{CQ}=\frac{3}{4}$,MN=3t,DN=10-7t,
∴$\frac{10-7t}{3t}=\frac{3}{4}$,
∴t=$\frac{40}{37}$,
即:使得△CMQ与△DMN相似的t的值为$\frac{10}{11}$或$\frac{40}{37}$.
点评 此题是相似形综合题,主要考查了正方形,矩形的性质,锐角三角函数,勾股定理,三角形的面积的计算方法,解本题的关键是判断出△CMQ与△DMN相似的两种可能,难点是每一种情况下,判断出对应点.


科目:初中数学 来源: 题型:解答题
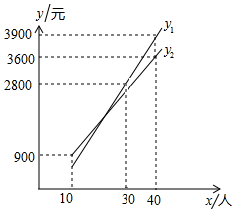 2016年3月28日,农业部发布了以“早春到乡村去踏青”为主题的219条休闲农业精品景点线路,其中河北省的“唐山迁西滨水度假游”等20条休闲农业精品线路入选.已知河北省某旅游景点的门票为a元/人,为吸引团队游客,对团队10人以上(包含10人)的游客实行动态票价:节假日期间门票不打折,但会在团队总费用的基础上有优惠;非节假日期间门票打b折.某团队在节假日期间的门票总费用y1(元)、非节假日期间的门票总费用y2(元)与团队人数x(人)(x≥10)之间的函数关系的图象如图所示.
2016年3月28日,农业部发布了以“早春到乡村去踏青”为主题的219条休闲农业精品景点线路,其中河北省的“唐山迁西滨水度假游”等20条休闲农业精品线路入选.已知河北省某旅游景点的门票为a元/人,为吸引团队游客,对团队10人以上(包含10人)的游客实行动态票价:节假日期间门票不打折,但会在团队总费用的基础上有优惠;非节假日期间门票打b折.某团队在节假日期间的门票总费用y1(元)、非节假日期间的门票总费用y2(元)与团队人数x(人)(x≥10)之间的函数关系的图象如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在平行四边形ABCD中,AC⊥AB,以C为圆心,CA为半径作圆弧交BC于点E,交CD的延长线于点F,以AC上一点O为圆心,OA为半径的圆与BC相切于点G,交AD于点N,若AC=6cm,OA=2cm,则图中阴影部分的面积为 $\frac{23}{3}π-5\sqrt{3}$,cm2(结果不取近似值).
如图,在平行四边形ABCD中,AC⊥AB,以C为圆心,CA为半径作圆弧交BC于点E,交CD的延长线于点F,以AC上一点O为圆心,OA为半径的圆与BC相切于点G,交AD于点N,若AC=6cm,OA=2cm,则图中阴影部分的面积为 $\frac{23}{3}π-5\sqrt{3}$,cm2(结果不取近似值).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,AC、BD为圆O的两条垂直的直径,动点P从圆心O出发,沿线段OC-$\widehat{CD}$-线段DO的路线作匀速运动,设运动时间为t秒,∠APB的度数为y度,则下列图象中表示y与t的函数关系最恰当的是( )
如图,AC、BD为圆O的两条垂直的直径,动点P从圆心O出发,沿线段OC-$\widehat{CD}$-线段DO的路线作匀速运动,设运动时间为t秒,∠APB的度数为y度,则下列图象中表示y与t的函数关系最恰当的是( )| A. | 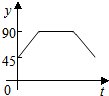 | B. | 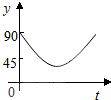 | C. | 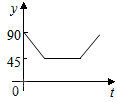 | D. | 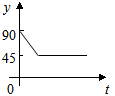 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com