
【题目】如图,正方形ABCD内有一点P,若PA=1,PB=2,PC=3.
(1)画出△ABP绕点B顺时针旋转90°得到的△CBE;
(2)求∠APB度数;
(3)求正方形ABCD的面积.

【答案】(1)画图见解析;(2)∠APB=135°;(3)正方形ABCD的面积为5+2![]() .
.
【解析】
(1)作∠QBC=∠ABP,BP=BQ=2,连接QC即可得出△BCQ;
(2)先由△BPQ是等腰直角三角形求出∠BQP的度数,再证明∠PQC=90°,即可得出∠BQC的度数,进而得出结论;
(3)如图,作CH⊥BQ交BQ的延长线于H.求出BH,CH,利用勾股定理即可解决问题.
(1)作∠QBC=∠ABP,BP=BQ=2,连接QC即可得出△BCQ;
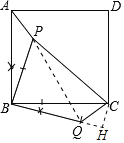
(2)连接PQ,
在Rt△PBQ中∵BP=BQ=2,
∴PQ2=BP2+BQ2=22+22=8,
在△PCQ中,
∵PC=3,QC=AP=1,
∴PC2=PQ2+QC2,
∴△PCQ是直角三角形,∠PQC=90°,
∵BP=BQ=2,∠PBQ=90°,
∴△PBQ是等腰直角三角形,
∴∠BQP=45°,
∵∠PQC=90°,
∴∠BQC=∠BQP+∠PQC=45°+90°=135°,
∵△BQC由△BPA旋转而成,
∴∠APB=∠BQC=135°.
(3)如图,作CH⊥BQ交BQ的延长线于H,
∵∠BQC=135°,
∴∠CQH=∠QCH=45°,
∴CH=QH,∵CQ=QP=1,
∴CH=QH=![]() ,
,
∴BH=BQ+QH=2+![]() ,
,
在Rt△BCH中,BC=![]() =
=![]() =
=![]() ,
,
∴正方形ABCD的面积为5+2![]() .
.


 春雨教育同步作文系列答案
春雨教育同步作文系列答案科目:初中数学 来源: 题型:
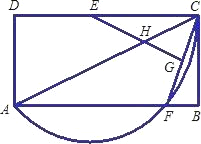
【题目】已知:如图,矩形ABCD中,点E、F分别在DC,AB边上,且点A、F、C在以点E为圆心,EC为半径的圆上,连接CF,作EG⊥CF于G,交AC于H.已知AB=6,设BC=x,AF=y.
(1)求证:∠CAB=∠CEG;
(2)①求y与x之间的函数关系式. ②x= 时,点F是AB的中点;
(3)当x为何值时,点F是![]() 的中点,以A、E、C、F为顶点的四边形是何种特殊四边形?试说明理由.
的中点,以A、E、C、F为顶点的四边形是何种特殊四边形?试说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
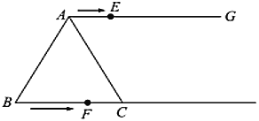
【题目】如图,在等边![]() 中,
中,![]() ,射线
,射线![]() ,点
,点![]() 从点
从点![]() 出发沿射线
出发沿射线![]() 以
以![]() 的速度运动,同时点
的速度运动,同时点![]() 从点
从点![]() 出发沿射线
出发沿射线![]() 以
以![]() 的速度运动,设点
的速度运动,设点![]() 运动的时间为
运动的时间为![]() .
.
(1)当点![]() 在线段
在线段![]() 上运动时,
上运动时,![]() _________
_________![]() ,当点
,当点![]() 在线段
在线段![]() 的延长线上运动时,
的延长线上运动时,![]() _________
_________![]() (请用含
(请用含![]() 的式子表示);
的式子表示);
(2)在整个运动过程中,当以点![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形是平行四边形时,求
为顶点的四边形是平行四边形时,求![]() 的值;
的值;
(3)求当![]() _________时,
_________时,![]() ,
,![]() 两点间的距离最小.
两点间的距离最小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)解方程x2﹣4x=12;
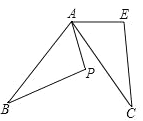
(2)如图,△ABP是由△ACE绕A点旋转得到的,若∠APB=110°,∠B=30°,∠PAC=20°,求旋转角的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD的对角线AC,BD相交于点O,过点O作OE⊥AC交AB于E,若BC=4,△AOE的面积为5,则sin∠BOE的值为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】方格纸中每个小正方形的边长都是单位1,△OAB在平面直角坐标系中的位置如图所示.解答问题:
(1)请按要求对△ABO作如下变换:
①将△OAB向下平移2个单位,再向左平移3个单位得到△O1A1B1;
②以点O为位似中心,位似比为2:1,将△ABC在位似中心的异侧进行放大得到△OA2B2.
(2)写出点A1,A2的坐标: , ;
(3)△OA2B2的面积为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
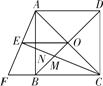
【题目】如图,正方形ABCD的对角线AC,BD相交于点O,延长CB至点F,使CF=CA,连接AF,∠ACF的平分线分别交AF,AB,BD于点E,N,M,连接EO.
(1)已知EO=![]() ,求正方形ABCD的边长;
,求正方形ABCD的边长;
(2)猜想线段EM与CN的数量关系并加以证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com