
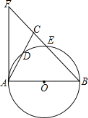
【题目】如图,在![]() 中,
中,![]() ,以
,以![]() 为直径的
为直径的![]() 分别交
分别交![]() 、
、![]() 于点
于点![]() 、
、![]() ,延长
,延长![]() 到点
到点![]() ,连接
,连接![]() ,使
,使![]() .
.
![]() 求证:
求证:![]() 是
是![]() 的切线;
的切线;
![]() 若
若![]() ,
,![]() ,求
,求![]() 的长.
的长.
【答案】![]() 证明见解析;
证明见解析;![]() 长为
长为![]() .
.
【解析】
(1)连接BD,由圆周角定理得出∠ADB=90°,由等腰三角形的性质得出∠ABC=2∠ABD,得出∠ABD=∠CAF,证出∠CAF+∠CAB=90°,BA⊥FA,即可得出结论;
(2)连接AE,由圆周角定理得出∠AEB=90°,设CE长为x,则EB长为3x,AB=BC=4x.由勾股定理可得AE=![]() x,在Rt△AEC中,由勾股定理得出方程,解方程即可.
x,在Rt△AEC中,由勾股定理得出方程,解方程即可.
![]() 连接
连接![]() ,如图
,如图![]() 所示:
所示:

∵![]() 是
是![]() 的直径
的直径
∴![]() ,
,
∵![]() ,
,
∴![]() 平分
平分![]() ,即
,即![]()
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,即
,即![]() ,
,
∴![]() 是
是![]() 的切线;
的切线;
![]() 连接
连接![]() ,如图
,如图![]() 所示:
所示:
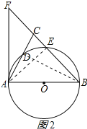
∵![]() 是
是![]() 的直径
的直径
∴![]() ,即
,即![]() 为直角三角形,
为直角三角形,
∵![]() ,
,
设![]() 长为
长为![]() ,则
,则![]() 长为
长为![]() ,
,![]() 长为
长为![]() .
.
则![]() 长为
长为![]() ,
,
在![]() 中由勾股定理可得
中由勾股定理可得![]() ,
,
在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,
由勾股定理得:![]() ,
,
解得:![]() ,
,
∵![]()
∴![]() ,即
,即![]() 长为
长为![]() .
.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:初中数学 来源: 题型:
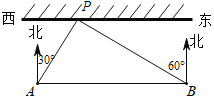
【题目】为了保证端午龙舟赛在我市汉江水域顺利举办,某部门工作人员乘快艇到汉江水域考察水情,以每秒10米的速度沿平行于岸边的赛道AB由西向东行驶.在A处测得岸边一建筑物P在北偏东30°方向上,继续行驶40秒到达B处时,测得建筑物P在北偏西60°方向上,如图所示,求建筑物P到赛道AB的距离(结果保留根号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,D是BC边上一点,AC=2,CD=1,设∠CAD=α.
(1)试写出α的四个三角函数值;
(2)若∠B=α,求BD的长?

查看答案和解析>>
科目:初中数学 来源: 题型:
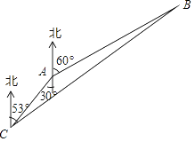
【题目】2016年12月底我国首艘航空母舰辽宁舰与数艘去驱航舰组成编队,携多架歼﹣15舰载战斗机和多型舰载直升机开展跨海区训练和试验任务,在某次演习中,预警直升机A发现在其北偏东60°,距离160千米处有一可疑目标B,预警直升机立即向位于南偏西30°距离40千米处的航母C报告,航母舰载战斗机立即升空沿北偏东53°方向向可疑目标飞去,请求出舰载战斗机到达目标的航程BC.
(结果保留整数,参考数据:sin53°≈0.8,cos53°≈0.6,tan53°≈1.3, ![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() 、
、![]() 的平分线分别交
的平分线分别交![]() 、
、![]() 于点
于点![]() 、
、![]() ,
,![]() 、
、![]() 相交于点
相交于点![]() ,连接
,连接![]() .下列结论:①
.下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④点
;④点![]() 到
到![]() 三个顶点的距离相等;⑤
三个顶点的距离相等;⑤![]() .其中正确的结论有( )个.
.其中正确的结论有( )个.
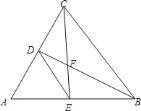
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某船以每小时![]() 海里的速度向正东方向航行,在点
海里的速度向正东方向航行,在点![]() 测得某岛
测得某岛![]() 在北偏东
在北偏东![]() 方向上,航行半小时后到达点
方向上,航行半小时后到达点![]() 测得该岛在北偏东
测得该岛在北偏东![]() 方向上,已知该岛周围
方向上,已知该岛周围![]() 海里内有暗礁.
海里内有暗礁.

![]() 说明点
说明点![]() 是否在暗礁区域内;
是否在暗礁区域内;
![]() 若继续向东航行有无触礁的危险?请说明理由.
若继续向东航行有无触礁的危险?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论中正确的是( )
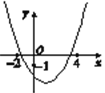
A. c>-1 B. b>0 C. 2a+b ≠0 D. 9a2+c>3b
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把一张矩形的纸ABCD沿对角线BD折叠,使点C落在点E处,BE与AD交于点F.
⑴求证:ΔABF≌ΔEDF;
⑵若将折叠的图形恢复原状,点F与BC边上的点M正好重合,连接DM,试判断四边形BMDF的形状,并说明理由.
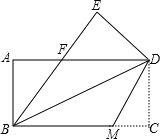
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD内有一点P,若PA=1,PB=2,PC=3.
(1)画出△ABP绕点B顺时针旋转90°得到的△CBE;
(2)求∠APB度数;
(3)求正方形ABCD的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com