
【题目】如图,矩形ABCD的对角线AC,BD相交于点O,过点O作OE⊥AC交AB于E,若BC=4,△AOE的面积为5,则sin∠BOE的值为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】C
【解析】由题意可知,OE为对角线AC的中垂线,则CE=AE=5,S△AEC=2S△AOE=10,由S△AEC求出线段AE的长度,进而在Rt△BCE中,由勾股定理求出线段BE的长度;然后证明∠BOE=∠BCE,从而可求得结果.
解:如图所示,连接EC.
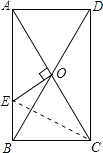
由题意可得,OE为对角线AC的垂直平分线,
∴CE=AE,S△AOE=S△COE=5,
∴S△AEC=2S△AOE=10.
∴![]() AEBC=10,又BC=4,
AEBC=10,又BC=4,
∴AE=5,
∴EC=5.
在Rt△BCE中,由勾股定理得:BE=![]() =3.
=3.
∵∠EBC+∠EOC=90°+90°=180°,
∴B、C、O、E四点共圆,
∴∠BOE=∠BCE.
(另解:∵∠AEO+∠EAO=90°,∠AEO=∠BOE+∠ABO,
∴∠BOE+∠ABO+∠EAO=90°,又∠ABO=90°-∠OBC=90°-(∠BCE+∠ECO)
∴∠BOE+(90°-(∠BCE+∠ECO))+∠EAO=90°,
化简得:∠BOE-∠BCE-∠ECO+∠EAO=0
∵OE为AC中垂线,
∴∠EAO=∠ECO.
代入上式得:∠BOE=∠BCE.)
∴sin∠BOE=sin∠BCE=![]() .
.
故答案为: ![]() .
.
“点睛”本题是几何综合题,考查了矩形性质、线段垂直平分线的性质、勾股定理、圆周角、三角函数的定义等知识点,有一定的难度.解题要点有两个:(1)求出线段AE的长度;(2)证明∠BOE=∠BCE.


科目:初中数学 来源: 题型:
【题目】将多项式a(x-y)+2by-2bx分解因式,正确的结果是( )
A. (x-y)(-a+2b) B. (x-y)(a+2b)
C. (x-y)(a-2b) D. -(x-y)(a+2b)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB、CD、EF相交于点O. 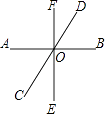
(1)写出∠COE的邻补角;
(2)分别写出∠COE和∠BOE的对顶角;
(3)如果∠BOD=60°,AB⊥EF,求∠DOF和∠FOC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】假期顾老师带学生乘车外出旅游,在乘车单价相同的情况下,甲、乙两位车主给出了不同的优惠方案.甲车主说“每人八折”,乙车主说“学生九折,老师免费”.李老师计算了一下,无论坐谁的车,费用都一样,则李老师带的学生为 ( )
A. 10名 B. 9名 C. 8名 D. 17名
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】每年的农历三月初一为通州风筝节.这天,小刘同学正在江海明珠广场上放风筝,如图风筝从A处起飞,几分钟后便飞达C处,此时,在AQ延长线上B处的小宋同学,发现自己的位置与风筝和广场边旗杆PQ的顶点P在同一直线上.
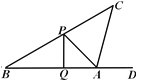
(1)已知旗杆高为10米,若在B处测得旗杆顶点P的仰角为30°,A处测得点P的仰角为45°,试求A、B之间的距离;
(2)此时,在A处背向旗杆又测得风筝的仰角为75°,若绳子在空中视为一条线段,求绳子AC为多少米?(结果可保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
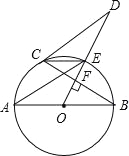
【题目】如图,AB是⊙O的直径,OD⊥弦BC于点F,交⊙O于点E,连结CE、AE、CD,若∠AEC=∠ODC.
(1)求证:直线CD为⊙O的切线;
(2)若AB=5,BC=4,求线段CD的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com