Question

【题目】如图，直线AB、CD、EF相交于点O．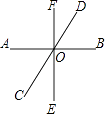
（1）写出∠COE的邻补角；
（2）分别写出∠COE和∠BOE的对顶角；
（3）如果∠BOD=60°，AB⊥EF，求∠DOF和∠FOC的度数．

Answer 1

【答案】
（1）解：∠COE的邻补角为∠COF和∠EOD
（2）解：∠COE和∠BOE的对顶角分别为∠DOF和∠AOF
（3）解：∵AB⊥EF，

∴∠AOF=∠BOF=90°，

∴∠DOF=∠BOF﹣∠BOD=90°﹣60°=30°，

又∵∠AOC=∠BOD=60°，

∴∠FOC=∠AOF+∠AOC=90°+60°=150°

【解析】（1）根据邻补角的定义即可得到结论；（2）根据对顶角的定义得到结论；（3）由垂直的定义得到∠AOF=∠BOF=90°，根据角的和差即可得到结论．
【考点精析】通过灵活运用对顶角和邻补角和垂线的性质，掌握两直线相交形成的四个角中，每一个角的邻补角有两个，而对顶角只有一个；垂线的性质：1、过一点有且只有一条直线与己知直线垂直．2、垂线段最短即可以解答此题．