练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】已知tanβ=22.3，则β=（精确到1″）

    【答案】87°25′56″
    【解析】∵tanβ=22.3，∴β=87°25′56″ ．
    故答案为：87°25′56″ ．
    利用计算器首先按2ndf ， 再按tan22.3，即可得出β的角度 ．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】x是数轴上任意一点表示的数，若|x﹣3|+|x+2|的值最小，则x的取值范围是（ ）

    A. x≥3B. x≤﹣2C. ﹣2≤x≤3D. ﹣2＜x＜3

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】“五·一”假期的某天，小明、小东两人同时分别从家出发骑共享单车到奥林匹克公园,已知小明家到公园的路程为15km，小东家到公园的路程为12km,小明骑车的平均速度比小东快3.5km/h,结果两人同时到达公园．求小东从家骑车到公园的平均速度.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】解答
    （1）如图（1），已知：在△ABC中，∠BAC=90°，AB=AC，直线m经过点A，BD⊥直线m，CE⊥直线m，垂足分别为点D、E．
    证明：DE=BD+CE．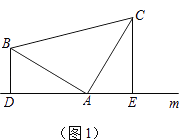

    （2）如图（2），将（1）中的条件改为：在△ABC中，AB=AC，D、A、E三点都在直线m上，并且有∠BDA=∠AEC=∠BAC=α，其中α为任意锐角或钝角．请问结论DE=BD+CE是否成立？如成立，请你给出证明；若不成立，请说明理由．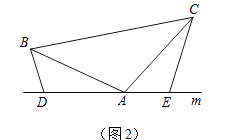

    （3）拓展与应用：如图（3），D、E是D、A、E三点所在直线m上的两动点（D、A、E三点互不重合），点F为∠BAC平分线上的一点，且△ABF和△ACF均为等边三角形，连接BD、CE，若∠BDA=∠AEC=∠BAC，试判断△DEF的形状．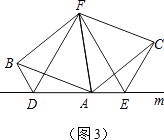

    查看答案和解析>>

    科目：初中数学 来源： 题型：

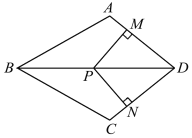
    【题目】如图，在四边形ABCD中，AB＝BC，对角线BD平分∠ABC，P是BD上一点，过点P作PM⊥AD，PN⊥CD，垂足分别为M，N.

    (1)求证：∠ADB＝∠CDB；

    (2)若∠ADC＝90°，求证：四边形MPND是正方形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图：在等边三角形ABC中，点E在线段AB上，点D在CB的延长线上，且AE=BD，试确定线段DE与EC的大小关系，并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知△ABC中，AB=AC，∠BAC=90°，直角∠EPF的顶点P是BC中点，两边PE，PF分别交AB，AC于点E，F，给出以下五个结论：①△PFA≌△PEB，②EF=AP，③△PEF是等腰直角三角形，④S四边形AEPF= S△ABC ， 当∠EPF在△ABC内绕顶点P旋转时（点E不与A，B重合），上述结论中始终正确有 （ ）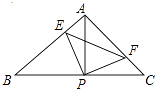

    A.1个
    B.2个
    C.3个
    D.4个

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】将多项式a（x-y）+2by-2bx分解因式，正确的结果是（ ）

    A. （x-y）（-a+2b） B. （x-y）（a+2b）

    C. （x-y）（a-2b） D. -（x-y）（a+2b）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，直线AB、CD、EF相交于点O．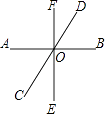
    （1）写出∠COE的邻补角；
    （2）分别写出∠COE和∠BOE的对顶角；
    （3）如果∠BOD=60°，AB⊥EF，求∠DOF和∠FOC的度数．

    查看答案和解析>>

    同步练习册答案