
【题目】如图,在四边形ABCD中,AB=BC,对角线BD平分∠ABC,P是BD上一点,过点P作PM⊥AD,PN⊥CD,垂足分别为M,N.
(1)求证:∠ADB=∠CDB;
(2)若∠ADC=90°,求证:四边形MPND是正方形.
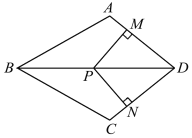
【答案】证明见解析.
【解析】
试题分析:(1)根据角平分线的性质和全等三角形的判定方法证明△ABD≌△CBD,由全等三角形的性质即可得到:∠ADB=∠CDB;
(2)若∠ADC=90°,由(1)中的条件可得四边形MPND是矩形,再根据两边相等的四边形是正方形即可证明四边形MPND是正方形.
试题解析:(1)∵对角线BD平分∠ABC,
∴∠ABD=∠CBD,
在△ABD和△CBD中,
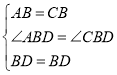 ,
,
∴△ABD≌△CBD(SAS),
∴∠ADB=∠CDB;
(2)∵PM⊥AD,PN⊥CD,
∴∠PMD=∠PND=90°,
∵∠ADC=90°,
∴四边形MPND是矩形,
∵∠ADB=∠CDB,
∴∠ADB=45°
∴PM=MD,
∴四边形MPND是正方形.


 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案科目:初中数学 来源: 题型:
【题目】已知一个角的两边与另一个角的两边分别平行,请结合图,探索这两个角之间的关系,并说明理由. 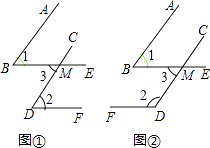
(1)如图①,AB∥CD,BE∥DF,∠1与∠2的关系是什么? 证明:
(2)如图②,AB∥CD,BE∥DF,∠1与∠2的关系是什么? 证明:
(3)经过上述证明,我们可得出结论,如果一个角的两边与另一个角的两边分别平行,那么这两个角
(4)若这两个角的两边分别平行,且一个角比另一个角的3倍少60°,则这两个角分别是多少度?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某书店老板去图书批发市场购买某种图书.第一次用1200元购书若干本,并按该书定价7元出售,很快售完.由于该书畅销,第二次购书时,每本书的批发价已比第一次提高了20%,他用1500元所购该书数量比第一次多10本.当按定价售出200本时,出现滞销,便以定价的4折售完剩余的书.试问该老板这两次售书总体上是赔钱了,还是赚钱了(不考虑其它因素)?若赔钱,赔多少?若赚钱,赚多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD和正方形OEFG中,点A和点F的坐标分别为 (3,2),(-1,-1),则两个正方形的位似中心的坐标是( )

A.(1,0)
B.(-5,-1)
C.(1,0)或(-5,-1)
D.(1,0)或(-5,-2)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com