
����Ŀ����֪һ���ǵ���������һ���ǵ����߷ֱ�ƽ�У�����ͼ��̽����������֮��Ĺ�ϵ����˵�����ɣ� 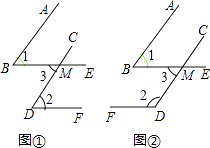
��1����ͼ�٣�AB��CD��BE��DF����1���2�Ĺ�ϵ��ʲô�� ֤����
��2����ͼ�ڣ�AB��CD��BE��DF����1���2�Ĺ�ϵ��ʲô�� ֤����
��3����������֤�������ǿɵó����ۣ����һ���ǵ���������һ���ǵ����߷ֱ�ƽ�У���ô��������
��4�����������ǵ����߷ֱ�ƽ�У���һ���DZ���һ���ǵ�3����60�㣬���������Ƿֱ��Ƕ��ٶȣ�
���𰸡�
��1�����
�⣺��1=��2��
֤�����£���AB��CD��
���1=��3��
��BE��DF��
���2=��3��
���1=��2
��2������
�⣺��1+��2=180�㣮
֤�����£���AB��CD��
���1=��3��
��BE��DF��
���2+��3=180�㣬
���1+��2=180�㣻
��3����Ȼ�
��4���⣺��һ���ǵĶ���Ϊx������һ���ǵĶ���Ϊ3x��60�㣬
��x=3x��60�㣬���x=30�㣬���������ǵĶ����ֱ�Ϊ30�㣬30�㣻
��x+3x��60��=180�㣬���x=60�㣬���������ǵĶ����ֱ�Ϊ60�㣬120��
����������1������ƽ���ߵ������á�1=��3����2=��3�����1=��2����2������ƽ���ߵ������á�1=��3����2+��3=180�㣬���ԡ�1+��2=180�㣻��3���ɣ�1���ͣ�2���Ľ��۽��лش𣻣�4����һ���ǵĶ���Ϊx������һ���ǵĶ���Ϊ3x��60�㣬���ݣ�3���Ľ��۽������ۣ�x=3x��60���x+3x��60��=180�㣬Ȼ��ֱ�ⷽ�����x����ɵõ���Ӧ�����ǵĶ�����
�����㾫��������ƽ���ߵ����ʶ���Ŀ�����жϼ��ɵõ��𰸣���Ҫ��֪��ֱ��ƽ�У�ͬλ����ȣ���ֱ��ƽ�У��ڴ�����ȣ���ֱ��ƽ�У�ͬ���ڽǻ�����


 �����ҵ��ٿ���������������ϵ�д�
�����ҵ��ٿ���������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ���ı���ABCD�У�AC��BD�ཻ�ڵ�O��AB��AC����DAC=45�㣬AC=2����BD�ij�Ϊ�� �� 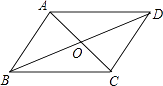
A.6
B.2 ![]()
C.![]()
D.3
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ü�������֤�����е�ʽ����ȷ���ǣ�������
A.sin18��24��+sin35��26��=sin54��
B.sin65��54��-sin35��54��=sin30��
C.2sin15��30��=sin31��
D.sin70��18��-sin12��18��=sin47��42��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����塤һ�����ڵ�ij�죬С����С������ͬʱ�ֱ�Ӽҳ����ﹲ������������ƥ�˹�,��֪С���ҵ�����·��Ϊ15km��С���ҵ�����·��Ϊ12km,С���ﳵ��ƽ���ٶȱ�С����3.5km/h,�������ͬʱ���﹫����С���Ӽ��ﳵ������ƽ���ٶ�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪M= ![]() ��m+3������ƽ������N=
��m+3������ƽ������N= ![]() ��n��2���������� ��M��N��ֵ��ƽ������
��n��2���������� ��M��N��ֵ��ƽ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����
��1����ͼ��1������֪���ڡ�ABC�У���BAC=90�㣬AB=AC��ֱ��m������A��BD��ֱ��m��CE��ֱ��m������ֱ�Ϊ��D��E��
֤����DE=BD+CE��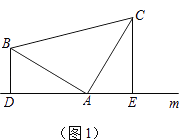
��2����ͼ��2��������1���е�������Ϊ���ڡ�ABC�У�AB=AC��D��A��E���㶼��ֱ��m�ϣ������С�BDA=��AEC=��BAC=�������Ц�Ϊ������ǻ�۽ǣ����ʽ���DE=BD+CE�Ƿ��������������������֤����������������˵�����ɣ� 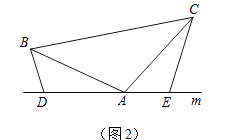
��3����չ��Ӧ�ã���ͼ��3����D��E��D��A��E��������ֱ��m�ϵ������㣨D��A��E���㻥���غϣ�����FΪ��BACƽ�����ϵ�һ�㣬�ҡ�ABF�͡�ACF��Ϊ�ȱ������Σ�����BD��CE������BDA=��AEC=��BAC�����жϡ�DEF����״�� 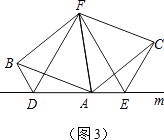
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����ı���ABCD�У�AB��BC���Խ���BDƽ����ABC��P��BD��һ�㣬����P��PM��AD��PN��CD������ֱ�ΪM��N.
(1)��֤����ADB����CDB��
(2)����ADC��90������֤���ı���MPND�������Σ�
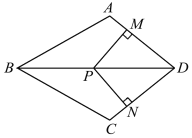
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��ABC�У�AB=AC����BAC=90�㣬ֱ�ǡ�EPF�Ķ���P��BC�е㣬����PE��PF�ֱ�AB��AC�ڵ�E��F����������������ۣ��١�PFA�ա�PEB����EF=AP���ۡ�PEF�ǵ���ֱ�������Σ���S�ı���AEPF= ![]() S��ABC �� ����EPF�ڡ�ABC���ƶ���P��תʱ����E����A��B�غϣ�������������ʼ����ȷ�� �� ��
S��ABC �� ����EPF�ڡ�ABC���ƶ���P��תʱ����E����A��B�غϣ�������������ʼ����ȷ�� �� �� 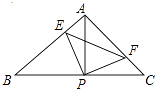
A.1��
B.2��
C.3��
D.4��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com