
【题目】如图,正方形ABCD和正方形OEFG中,点A和点F的坐标分别为 (3,2),(-1,-1),则两个正方形的位似中心的坐标是( )

A.(1,0)
B.(-5,-1)
C.(1,0)或(-5,-1)
D.(1,0)或(-5,-2)
【答案】D
【解析】
试题分析:考查位似变换中对应点的坐标的变化规律.本题应分两种情况讨论,一种是E和C是对应点,G和A是对应点;二种是A和E是对应点,C和G是对应点.
解:∵正方形ABCD和正方形OEFG中A和点F的坐标分别为(3,2),(﹣1,﹣1),
∴E(﹣1,0)、G(0,﹣1)、D(5,2)、B(3,0)、C(5,0),
(1)当E和C是对应顶点,G和A是对应顶点时,位似中心就是EC与AG的交点,
设AG所在直线的解析式为y=kx+b(k≠0),
∴![]() ,解得
,解得![]() .
.
∴此函数的解析式为y=x﹣1,与EC的交点坐标是(1,0);
(2)当A和E是对应顶点,C和G是对应顶点时,位似中心就是AE与CG的交点,
设AE所在直线的解析式为y=kx+b(k≠0),
![]() ,解得
,解得![]() ,故此一次函数的解析式为y=
,故此一次函数的解析式为y=![]() x+
x+![]() …①,
…①,
同理,设CG所在直线的解析式为y=kx+b(k≠0),
![]() ,解得
,解得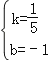 ,
,
故此直线的解析式为y=![]() x﹣1…②
x﹣1…②
联立①②得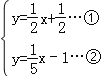
解得![]() ,故AE与CG的交点坐标是(﹣5,﹣2).
,故AE与CG的交点坐标是(﹣5,﹣2).
故答案为:(1,0)、(﹣5,﹣2).


科目:初中数学 来源: 题型:
【题目】用计算器验证,下列等式中正确的是( )
A.sin18°24′+sin35°26′=sin54°
B.sin65°54′-sin35°54′=sin30°
C.2sin15°30′=sin31°
D.sin70°18′-sin12°18′=sin47°42′
查看答案和解析>>
科目:初中数学 来源: 题型:
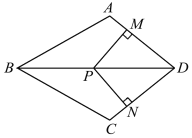
【题目】如图,在四边形ABCD中,AB=BC,对角线BD平分∠ABC,P是BD上一点,过点P作PM⊥AD,PN⊥CD,垂足分别为M,N.
(1)求证:∠ADB=∠CDB;
(2)若∠ADC=90°,求证:四边形MPND是正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC中点,两边PE,PF分别交AB,AC于点E,F,给出以下五个结论:①△PFA≌△PEB,②EF=AP,③△PEF是等腰直角三角形,④S四边形AEPF= ![]() S△ABC , 当∠EPF在△ABC内绕顶点P旋转时(点E不与A,B重合),上述结论中始终正确有 ( )
S△ABC , 当∠EPF在△ABC内绕顶点P旋转时(点E不与A,B重合),上述结论中始终正确有 ( ) 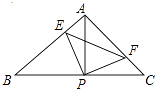
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将多项式a(x-y)+2by-2bx分解因式,正确的结果是( )
A. (x-y)(-a+2b) B. (x-y)(a+2b)
C. (x-y)(a-2b) D. -(x-y)(a+2b)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com