
【题目】在△ABC中,AE平分∠BAC交BC于E,DE∥AC交AB于D,过D作DF∥BC交AC于F,若AD=3,求FC. 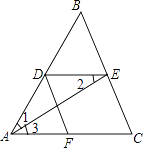
科目:初中数学 来源: 题型:
【题目】已知整数a1 , a2 , a3 , a4…满足下列条件:a1=0,a2=﹣|a1+1|,a3=﹣|a2+2|,a4=﹣|a3+3|…依此类推,则a2017的值为( )
A.﹣1009
B.﹣1008
C.﹣2017
D.﹣2016
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算
(1)﹣4﹣28﹣(﹣19)+(﹣24)
(2)(﹣ ![]() )﹣(﹣1
)﹣(﹣1 ![]() )﹣(﹣1
)﹣(﹣1 ![]() )﹣(+1.75).
)﹣(+1.75).
(3)( ![]() +
+ ![]() ﹣
﹣ ![]() )×(﹣60)
)×(﹣60)
(4)﹣14﹣ ![]() ×[1﹣(﹣3)2].
×[1﹣(﹣3)2].
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】x是数轴上任意一点表示的数,若|x﹣3|+|x+2|的值最小,则x的取值范围是( )
A. x≥3B. x≤﹣2C. ﹣2≤x≤3D. ﹣2<x<3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,是一个长为2m、宽为2n的长方形,沿图中虚线剪成四个完全一样的小长方形,然后按图2的形状拼成一个正方形. 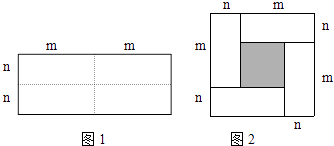
(1)图2中阴影部分的面积为;
(2)用两种不同的方法计算图2中阴影部分的面积,可以得到的等式是(只填序号); ①(m+n)2=m2+2mn+n2 ②(m﹣n)2=m2﹣2mn+n2③(m﹣n)2=(m+n)2﹣4mn
(3)若x﹣y=﹣4,xy= ![]() ,则x+y= .
,则x+y= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用计算器验证,下列等式中正确的是( )
A.sin18°24′+sin35°26′=sin54°
B.sin65°54′-sin35°54′=sin30°
C.2sin15°30′=sin31°
D.sin70°18′-sin12°18′=sin47°42′
查看答案和解析>>
科目:初中数学 来源: 题型:
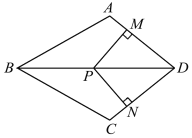
【题目】如图,在四边形ABCD中,AB=BC,对角线BD平分∠ABC,P是BD上一点,过点P作PM⊥AD,PN⊥CD,垂足分别为M,N.
(1)求证:∠ADB=∠CDB;
(2)若∠ADC=90°,求证:四边形MPND是正方形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com