练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】正比例函数y=x与反比例函数y=的图象相交于A、C两点．AB⊥x轴于B，CD⊥x轴于D（如图），则四边形ABCD的面积为（ ）

    A．1 B． C．2 D．

    【答案】C

    【解析】

    试题分析：首先根据反比例函数图象上的点与原点所连的线段、坐标轴、向坐标轴作垂线所围成的直角三角形面积S的关系即S=|k|，得出S△AOB=S△ODC=，再根据反比例函数的对称性可知：OB=OD，得出S△AOB=S△ODA，S△ODC=S△OBC，最后根据四边形ABCD的面积=S△AOB+S△ODA+S△ODC+S△OBC，得出结果．

    解：根据反比例函数的对称性可知：OB=OD，AB=CD，

    ∴四边形ABCD的面积=S△AOB+S△ODA+S△ODC+S△OBC=1×2=2．

    故选C．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

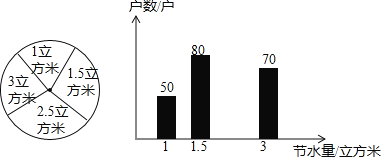
    【题目】 “节约用水、人人有责”，某班学生利用课余时间对金辉小区300户居民的用水情况进行了统计，发现5月份各户居民的用水量比4月份有所下降，并且将5月份各户居民的节水量统计整理成如图所示的统计图表

    节水量/立方米

    1

    1.5

    2.5

    3

    户数/户

    50

    80

    a

    70

    （1）写出统计表中a的值和扇形统计图中2.5立方米对应扇形的圆心角度数．

    （2）根据题意，将5月份各居民的节水量的条形统计图补充完整．

    （3）求该小区300户居民5月份平均每户节约用水量，若用每立方米水需4元水费，请你估算每户居民1年可节约多少元钱的水费？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】二次函数 y=ax2+bx+c（a≠0）的图象经过点A（4，0），B（2，8），且以x=1为对称轴．

    （1）求此函数的解析式，并作出它的示意图；

    （2）当0＜x＜4时，写出y的取值范围；

    （3）结合图象直接写出不等式ax2+bx+c＞0（a≠0）的解集．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】以下列各组线段为边能构成三角形的是（ ）

    A. 3 cm，2 cm，5 cm B. 7 cm，3 cm，3 cm

    C. 8 cm，10 cm，20 cm D. 4 cm，5 cm，6 cm

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】你对“0”有多少了解？下列关于“0”的说法错误的是（ 　　）

    A. 任何数与0相乘都得0 B. 0是最小的有理数

    C. 绝对值最小的有理数是0 D. 0没有倒数

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如果 mx2 + 4x + m2 + 3 = 0 是一个完全平方式，则 m 的值是( )

    A. m=±1

    B. m=－1

    C. m=0

    D. m=1

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】五种几何体：①正方体，②球，③圆锥，④圆柱，⑤三棱柱．

    从正面，从左面，从上面看到的形状图完全相同的几何体是_____________（填序号即可）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某中学举行了一次“世博”知识竞赛．赛后抽取部分参赛同学的成绩进行整理，并制作成图表如下：

    请根据以上图表提供的信息，解答下列问题：

    （1）写出表格中m和n所表示的数：m= ，n= ，并补全频数分布直方图；

    （2）抽取部分参赛同学的成绩的中位数落在第 组；

    （3）如果比赛成绩80分以上（含80分）可以获得奖励，那么获奖率是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】一个几何体从上面看是圆，从左面和正面看是长方形，则该几何体是（ ）

    A. 正方体 B. 圆锥 C. 圆柱 D. 球

    查看答案和解析>>

    同步练习册答案