
【题目】如图,将ABCD的边DC延长到点E,使CE=DC,连接AE,交BC于点F.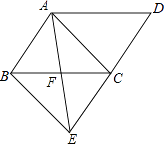
(1)求证:△ABF≌△ECF;
(2)若∠AFC=2∠D,连接AC、BE.求证:四边形ABEC是矩形.
【答案】
(1)证明:∵四边形ABCD是平行四边形,
∴AB∥DC,AB=DC,
∴∠ABF=∠ECF,
∵EC=DC,∴AB=EC,
在△ABF和△ECF中,
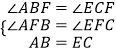 ,
,
∴△ABF≌△ECF(AAS)
(2)证明:∵AB=EC,AB∥EC,
∴四边形ABEC是平行四边形,
∴FA=FE,FB=FC,
∵四边形ABCD是平行四边形,
∴∠ABC=∠D,
又∵∠AFC=2∠D,
∴∠AFC=2∠ABC,
∵∠AFC=∠ABC+∠BAF,
∴∠ABC=∠BAF,
∴FA=FB,
∴FA=FE=FB=FC,
∴AE=BC,
∴四边形ABEC是矩形
【解析】(1)先平行四边形的对边平行且相等可证明AB∥CE,且AB=CE,然后依据平行线的性质可证明∠ABF=∠ECF,最后,依据AAS可证明△ABF≌△ECF;
(2)由(1)得的结论先证得四边形ABEC是平行四边形,通过角的关系得出FA=FB,从而可证明AE=BC,故此可证明四边形ABEC为矩形.


科目:初中数学 来源: 题型:
【题目】如图,D,E分别是AB,AC的中点,BE是∠ABC的平分线,对于下列结论:①BC=2DE;②DE∥BC;③BD=DE;④BE⊥AC.其中正确的是 ( )
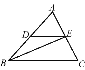
A. ①② B. ①②③ C. ①②④ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面说法错误的是( )
A.过一点有且只有一条直线与已知直线垂直.
B.在同一个平面内,任意三条直线相交,交点的个数最多有3个
C.平行于同一直线的两条直线平行.
D.两条平行线被第三条直线所截,一对内错角的平分线互相平行.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC=90°,AD是中线,E是AD的中点,过点A作AF∥BC交BE的延长线于F,连接CF.

(1)求证:AD=AF;
(2)如果AB=AC,试判断四边形ADCF的形状,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在Rt△ABC中,∠C=90°,AC=8cm,BC=6cm.直线PE从B点出发,以2cm/s的速度向点A方向运动,并始终与BC平行,与AC交于点E.同时,点F从C点出发,以1cm/s的速度沿CB向点B运动,设运动时间为t (s)(0<t<5).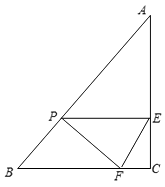
(1)当t为何值时,四边形PFCE是矩形?
(2)设△PEF的面积为S(cm2),求S与t的函数关系式;
(3)是否存在某一时刻t,使△PEF的面积是△ABC面积的 ![]() ?若存在,求出t的值;若不存在,请说明理由.
?若存在,求出t的值;若不存在,请说明理由.
(4)连接BE,是否存在某一时刻t,使PF经过BE的中点?若存在,求出t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校1200名学生参加了一场“安全知识”问答竞赛活动,为了解笔试情况,随机抽查了部分学生的得分情况,整理并制作了如图所示的图表(部分未完成),请根据图表提供的信息,解答下列问题:
分数段 | 频数 | 频率 |
| 30 | 0.1 |
| 90 |
|
|
| 0.4 |
| 60 | 0.2 |
(Ⅰ)本次调查的样本容量为______;
(Ⅱ)在表中,![]() ______,
______,![]() ______;
______;
(Ⅲ)补全频数分布直方图;

(Ⅳ)如果比赛成绩80分以上(含80分)为优秀,本次竞赛中笔试成绩为优秀的大约有多少名学生?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有四张背面完全相同的纸牌A、B、C、D,其正面分别画有四个不同的几何图形,将这四张纸牌背面朝上洗匀.
(1)从中随机摸出一张,求摸出的牌面图形是中心对称图形的概率;
(2)小明和小亮约定做一个游戏,其规则为:先由小明随机摸出一张纸牌,不放回,再由小亮从剩下的纸牌中随机摸出一张,若摸出的两张牌面图形都是轴对称图形小明获胜,否则小亮获胜,这个游戏公平吗?请用列表法(或树状图)说明理由(纸牌用A、B、C、D表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=3cm,BC=6cm.点P从点D出发向点A运动,运动到点A即停止;同时,点Q从点B出发向点C运动,运动到点C即停止,点P、Q的速度都是1cm/s.连接PQ、AQ、CP.设点P、Q运动的时间为ts.
当t为何值时,四边形ABQP是矩形;
当t为何值时,四边形AQCP是菱形;
分别求出(2)中菱形AQCP的周长和面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com