
����Ŀ����֪����ͼ����Rt��ABC�У���C=90�㣬AC=8cm��BC=6cm��ֱ��PE��B���������2cm/s���ٶ����A�����˶�����ʼ����BCƽ�У���AC���ڵ�E��ͬʱ����F��C���������1cm/s���ٶ���CB���B�˶������˶�ʱ��Ϊt ��s����0��t��5����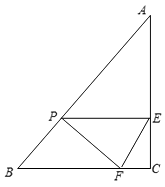
��1����tΪ��ֵʱ���ı���PFCE�Ǿ��Σ�
��2�����PEF�����ΪS��cm2������S��t�ĺ�����ϵʽ��
��3���Ƿ����ijһʱ��t��ʹ��PEF������ǡ�ABC����� ![]() �������ڣ����t��ֵ���������ڣ���˵�����ɣ�
�������ڣ����t��ֵ���������ڣ���˵�����ɣ�
��4������BE���Ƿ����ijһʱ��t��ʹPF����BE���е㣿�����ڣ����t��ֵ���������ڣ���˵�����ɣ�
���𰸡�
��1���⣺��Rt��ABC�У��ߡ�C=90�㣬AC=8��BC=6��
��AB= ![]() =
= ![]() =10��
=10��
��PE��BC��
�� ![]() =
= ![]() =
= ![]() ��
��
�� ![]() =
= ![]() =
= ![]() ��
��
��PE= ![]() ��10��2t����AE=
��10��2t����AE= ![]() ��10��2t����
��10��2t����
��PE=CFʱ���ı���PECF�Ǿ��Σ�
�� ![]() ��10��2t��=t��
��10��2t��=t��
���t= ![]()
��2���⣺S= ![]() PECE=
PECE= ![]() ��
�� ![]() ��10��2t����[8��
��10��2t����[8�� ![]() ��10��2t��]=��
��10��2t��]=�� ![]() t2+
t2+ ![]() t
t
��3���⣺������ڣ������⩁ ![]() t2+
t2+ ![]() t=
t= ![]() ��
�� ![]() ��6��8��
��6��8��
������t2��5t=5=0��
���t= ![]() ��
��
��t= ![]() ʱ����PEF������ǡ�ABC�����
ʱ����PEF������ǡ�ABC����� ![]()
��4���⣺��PE=BFʱ��PF����BE���е㣮
���� ![]() ��10��2t��=6��t��
��10��2t��=6��t��
���t=0���������⣬
�����ijһʱ��t��ʹPF����BE���е㣮
����������1���������ݹ��ɶ������AB�ij���Ȼ����PE��BC���ɵõ���APE�ס�ABC���������������ε����ʿɵõ�PE��t�Ĺ�ϵʽ������ɵ�PE=CFʱ���ı���PECF�Ǿ��Σ��г�������⼴�ɣ�
��2���ɣ�1���ɵõ�PE��CE�ij���Ȼ���ٸ���S=![]() ,PECE���㼴�ɣ�
,PECE���㼴�ɣ�
��3��������ڣ�Ȼ���ɡ�PEF�����=��ABC�����![]() �з�����⼴��.
�з�����⼴��.
��4����PE=BFʱ��PF����BE���е㣮����![]() ��10-2t��=6-t���Ӷ��������ж�.
��10-2t��=6-t���Ӷ��������ж�.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ��������������������Ů����ѡ������ͬѧ����У�����������ݳ�ר���������ˣ���ѡ����ǡΪһ��һŮ�ĸ����� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУΪ������Ӧ���Ͽ�ʥ�أ���������������Ʒ�ƽ��裬��ÿ������������ڿο�չ�˷ḻ��ʵ��߰�ѡ�λ.�����ۺ�ʵ���������������������֪������˼��������������Դ�������ſγ̣�Ҫ��ȫУѧ�������������һ�ſγ�.Ϊ�˽�ѧ�������ۺ�ʵ����γ̻����������ȡ�˲���ѧ�����е��飬���ݵ�������������ͼ��ʾ������������ͳ��ͼ������ͳ��ͼ.

��1�����ʱ������ȡ��ѧ�����ж�����?����ȫ����ͳ��ͼ.
��2��������ͳ��ͼ�У���ѡ�����������γ̵�ѧ����������Ӧ������Բ�ĽǵĶ���.
��3������У����ѧ��1200�ˣ��������в�������Դ���γ̵�ѧ�����ж����ˣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
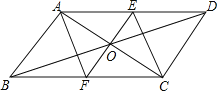
����Ŀ����ͼ����ƽ���ı���ABCD�У��Խ���AC��BD���ڵ�O������O��ֱ��EF�ֱ���AD��BC���ڵ�E��F��EF��AC������AF��CE��
��1����֤��OE=OF��
��2�����ж��ı���AECF��ʲô�����ı��Σ���֤����Ľ��ۣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABCD�ı�DC�ӳ�����E��ʹCE=DC������AE����BC�ڵ�F��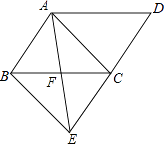
��1����֤����ABF�ա�ECF��
��2������AFC=2��D������AC��BE����֤���ı���ABEC�Ǿ��Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��(1����:![]() ��
��
(2)�ⲻ��ʽ��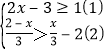
�����������,��ɱ���Ľ��:
�ⲻ��ʽ(1),��______________.
�ⲻ��ʽ(2),��_______________.
�Ѳ���ʽ(1)��(2)�Ľ⼯�������ϱ�ʾ����
![]()
��ԭ����ʽ��Ľ⼯Ϊ_________________.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ�����ǰ��е�����ֱ�������ε�ֱ�Ƕ���0��ͼ1��ʽ������һ��(���С�C��30�㣬��CDO��60�㣻��OAB����OBA��45��).��COD���ŵ�O˳ʱ����תһ�ܣ���ת���ٶ�Ϊÿ��10�㣬����תʱ��Ϊt�룬��ش��������⣺(��ֱ��д����)
(1)��0��t��9ʱ(��ͼ2)����BOC���AOD�к�������ϵ
(2)��tΪ��ֵʱ����OA��CD��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������3��3������ͼ������9����ͬ��С���������,ÿ������ͼ����3��С��������Ϳ����Ӱ,�������µ�6���հ�С��������,������Ҫ��Ϳ����Ӱ:
(1)����ͼ1��ѡȡ1��Ϳ����Ӱ,ʹ4����ӰС���������һ����Գ�ͼ��,���������ĶԳ�ͼ��;
(2)����ͼ2��ѡȡ1��Ϳ����Ӱ,ʹ4����ӰС���������һ�����ĶԳ�ͼ��,��������Գ�ͼ��;
(3)����ͼ3��ѡȡ2��Ϳ����Ӱ,ʹ5����ӰС���������һ����Գ�ͼ��.
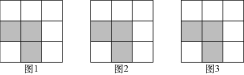
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У���D��E�ֱ�ΪAB��AC���е㣬���ADE���ı���BCED�������Ϊ�� ��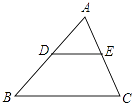
A.1��1
B.1��2
C.1��3
D.1��4
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com