
【题目】某校为积极响应“南孔圣地,衢州有礼”城市品牌建设,在每周五下午第三节课开展了丰富多彩的走班选课活动.其中综合实践类共开设了“礼行”“礼知”“礼思”“礼艺”“礼源”等五门课程,要求全校学生必须参与其中一门课程.为了解学生参与综合实践类课程活动情况,随机抽取了部分学生进行调查,根据调查结果绘制了如图所示不完整的条形统计图和扇形统计图.

(1)请问被随机抽取的学生共有多少名?并补全条形统计图.
(2)在扇形统计图中,求选择“礼行”课程的学生人数所对应的扇形圆心角的度数.
(3)若该校共有学生1200人,估计其中参与“礼源”课程的学生共有多少人?
【答案】(1)学生共有40人,条形统计图如图所示.见解析;(2)选“礼行”课程的学生所对应的扇形圆心角的度数为36°;(3)解:参与“礼源”课程的学生约有240人.
【解析】
(1)根据统计表和扇形统计图中的数据,由总数=频数÷频率,![]() 即可得答案.(2)由条形统计图中可得“礼行”学生人数,由
即可得答案.(2)由条形统计图中可得“礼行”学生人数,由![]() ×360°,计算即可求得答案.(3)由条形统计图知“礼源”的学生人数,根据
×360°,计算即可求得答案.(3)由条形统计图知“礼源”的学生人数,根据![]() ×全校总人数,计算即可求得答案.
×全校总人数,计算即可求得答案.
(1)解::(1)被随机抽取的学生共有12÷30%=40(人),
则礼艺的人数为40×15%=6(人),
补全图形如下:

(2)解:选“礼行”课程的学生所对应的扇形圆心角的度数为![]()
(3)解:参与“礼源”课程的学生约有![]() (人)
(人)


科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠ACB=90°,∠A=30°,BD是△ABC的角平分线,DE⊥AB于点E.

(1)如图1,连接EC,求证:△EBC是等边三角形;
(2)点M是线段CD上的一点(不与点C,D重合),以BM为一边,在BM的下方作∠BMG=60°,MG交DE延长线于点G.请你在图2中画出完整图形,并直接写出MD,DG与AD之间的数量关系;
(3)如图3,点N是线段AD上的一点,以BN为一边,在BN的下方作∠BNG=60°,NG交DE延长线于点G.试探究ND,DG与AD数量之间的关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
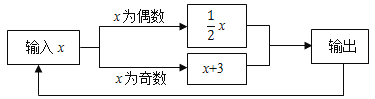
【题目】如图所示的运算程序中,若开始输入的x值为7,我们发现第1次输出的结果为10,第2次输出的结果为5,……,第2019次输出的结果为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】推理填空:
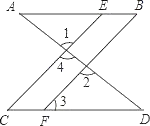
如图,已知∠1=∠2,∠B=∠C,可推得AB∥CD.理由如下:
∵∠1=∠2(已知),且∠1=∠4( )
∴∠2=∠4 (等量代换)
∴CE∥BF ( )
∴∠ =∠3( )
又∵∠B=∠C(已知),∴∠3=∠B(等量代换)
∴AB∥CD ( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面说法错误的是( )
A.过一点有且只有一条直线与已知直线垂直.
B.在同一个平面内,任意三条直线相交,交点的个数最多有3个
C.平行于同一直线的两条直线平行.
D.两条平行线被第三条直线所截,一对内错角的平分线互相平行.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在Rt△ABC中,∠C=90°,AC=8cm,BC=6cm.直线PE从B点出发,以2cm/s的速度向点A方向运动,并始终与BC平行,与AC交于点E.同时,点F从C点出发,以1cm/s的速度沿CB向点B运动,设运动时间为t (s)(0<t<5).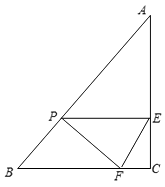
(1)当t为何值时,四边形PFCE是矩形?
(2)设△PEF的面积为S(cm2),求S与t的函数关系式;
(3)是否存在某一时刻t,使△PEF的面积是△ABC面积的 ![]() ?若存在,求出t的值;若不存在,请说明理由.
?若存在,求出t的值;若不存在,请说明理由.
(4)连接BE,是否存在某一时刻t,使PF经过BE的中点?若存在,求出t的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com