
【题目】如图,已知AB=AD,∠ABC=∠ADC.试判断AC与BD的位置关系,并说明理由.

【答案】AC⊥BD,理由见解析.
【解析】
AC与BD垂直,理由为:由AB=AD,利用等边对等角得到一对角相等,利用等式性质得到∠BDC=∠DBC,利用等角对等边得到DC=BC,利用SSS得到三角形ABC与三角形ADC全等,利用全等三角形对应角相等得到∠DAC=∠BAC,再利用三线合一即可得证.
AC⊥BD,理由为:
∵AB=AD(已知),
∴∠ADB=∠ABD(等边对等角),
∵∠ABC=∠ADC(已知),
∴∠ABC﹣∠ABD=∠ADC﹣∠ADB(等式性质),
即∠BDC=∠DBC,
∴DC=BC(等角对等边),
在△ABC和△ADC中,
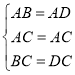
∴△ABC≌△ADC(SSS),
∴∠DAC=∠BAC(全等三角形的对应角相等),
又∵AB=AD,
∴AC⊥BD(等腰三角形三线合一).


科目:初中数学 来源: 题型:
【题目】某校为积极响应“南孔圣地,衢州有礼”城市品牌建设,在每周五下午第三节课开展了丰富多彩的走班选课活动.其中综合实践类共开设了“礼行”“礼知”“礼思”“礼艺”“礼源”等五门课程,要求全校学生必须参与其中一门课程.为了解学生参与综合实践类课程活动情况,随机抽取了部分学生进行调查,根据调查结果绘制了如图所示不完整的条形统计图和扇形统计图.

(1)请问被随机抽取的学生共有多少名?并补全条形统计图.
(2)在扇形统计图中,求选择“礼行”课程的学生人数所对应的扇形圆心角的度数.
(3)若该校共有学生1200人,估计其中参与“礼源”课程的学生共有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一副三角板中的两块直角三角形的直角顶点0按图1方式叠放在一起(其中∠C=30°,∠CDO=60°;∠OAB=∠OBA=45°).△COD绕着点O顺时针旋转一周,旋转的速度为每秒10°,若旋转时间为t秒,请回答下列问题:(请直接写出答案)
(1)当0<t<9时(如图2),∠BOC与∠AOD有何数量关系
(2)当t为何值时,边OA∥CD?

查看答案和解析>>
科目:初中数学 来源: 题型:
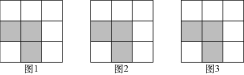
【题目】下列3×3的网格图都是由9个相同的小正方形组成,每个网格图中有3个小正方形已涂上阴影,请在余下的6个空白小正方形中,按下列要求涂上阴影:
(1)请在图1中选取1个涂上阴影,使4个阴影小正方形组成一个轴对称图形,但不是中心对称图形;
(2)请在图2中选取1个涂上阴影,使4个阴影小正方形组成一个中心对称图形,但不是轴对称图形;
(3)请在图3中选取2个涂上阴影,使5个阴影小正方形组成一个轴对称图形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在下列说法中:①过一点有且只有一条直线与已知直线平行;②-0.9是0.81的平方根;③若在平面直角坐标系中直线![]() 垂直于
垂直于![]() 轴,则直线
轴,则直线![]() 上所有的点的横坐标相同;④
上所有的点的横坐标相同;④![]() 是一个负数;⑤0的相反数和倒数都是0;⑥
是一个负数;⑤0的相反数和倒数都是0;⑥![]() ;⑦
;⑦![]() ;⑧全体有理数和数轴上的点一一对应.以上真命题的序号是__________.
;⑧全体有理数和数轴上的点一一对应.以上真命题的序号是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() 平分
平分![]() ,过点
,过点![]() 作
作![]() ,
,![]() 交
交![]() 于点
于点![]() ,
,![]() 交
交![]() 于点
于点![]() ,作
,作![]() 的平分线
的平分线![]() 交
交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,若
,若![]() ,下列结论:①
,下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ;⑤
;⑤![]() .其中正确的个数是( )
.其中正确的个数是( )

A.2B.3C.4D.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)请用两种不同的方法列代数式表示图1中阴影部分的面积.

方法①: ;
方法②: ;
(2)根据(1)写出一个等式: ;
(3)若x+y=8,xy=3.75,利用(2)中的结论,求x,y;
(4)有许多代数恒等式可以用图形的面积来表示.如图2,它表示了(2m+n)(m+n)=2m2+3mn+n2.试画出一个几何图形,使它的面积能表示(2m+n)(m+2n)=2m2+5mn+2n2.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com