
°ĺŐ‚ńŅ°Ņ»ÁÕľ£¨Ň◊őÔŌŖy=ax2+bx©Ā2Ķń∂‘≥∆÷Š «÷ĪŌŖx=1£¨”Žx÷ŠĹĽ”ŕA£¨BŃĹĶ„£¨”Žy÷ŠĹĽ”ŕĶ„C£¨Ķ„AĶń◊ÝĪÍő™£®©Ā2£¨0£©£¨Ķ„Pő™Ň◊őÔŌŖ…ŌĶń“ĽłŲ∂ĮĶ„£¨ĻżĶ„P◊ųPD°Õx÷Š”ŕĶ„D£¨ĹĽ÷ĪŌŖBC”ŕĶ„E£ģ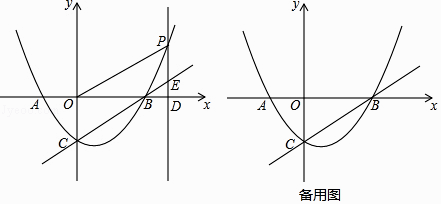
£®1£©«ůŇ◊őÔŌŖĹ‚őŲ Ĺ£Ľ
£®2£©»ŰĶ„P‘ŕĶŕ“ĽŌůŌřńŕ£¨ĶĪOD=4PE Ī£¨«ůňńĪŖ–őPOBEĶń√śĽż£Ľ
£®3£©‘ŕ£®2£©ĶńŐűľĢŌ¬£¨»ŰĶ„Mő™÷ĪŌŖBC…Ō“ĽĶ„£¨Ķ„Nő™∆Ĺ√ś÷ĪĹ«◊ÝĪÍŌĶńŕ“ĽĶ„£¨ «∑Ůīś‘ŕ’‚—ýĶńĶ„MļÕĶ„N£¨ ĻĶ√“‘Ķ„B£¨D£¨M£¨Nő™∂•Ķ„ĶńňńĪŖ–ő «Ń‚–ő£Ņ»Űīś‘ŕ…Ō£¨÷ĪĹ”–ī≥ŲĶ„NĶń◊ÝĪÍ£Ľ»Ű≤Ľīś‘ŕ£¨«ŽňĶ√ųņŪ”…£ģ
°ĺīūįł°Ņ
£®1£©
Ĺ‚£ļ°ŖŇ◊őÔŌŖy=ax2+bx©Ā2Ķń∂‘≥∆÷Š «÷ĪŌŖx=1£¨A£®©Ā2£¨0£©‘ŕŇ◊őÔŌŖ…Ō£¨°ŗ 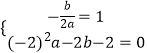 £¨Ĺ‚Ķ√£ļ
£¨Ĺ‚Ķ√£ļ 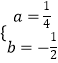 £¨Ň◊őÔŌŖĹ‚őŲ Ĺő™y=
£¨Ň◊őÔŌŖĹ‚őŲ Ĺő™y= ![]() x2©Ā
x2©Ā ![]() x©Ā2£Ľ
x©Ā2£Ľ
£®2£©
Ĺ‚£ļŃÓy= ![]() x2©Ā
x2©Ā ![]() x©Ā2=0£¨Ĺ‚Ķ√£ļx1=©Ā2£¨x2=4£¨ĶĪx=0 Ī£¨y=©Ā2£¨°ŗB£®4£¨0£©£¨C£®0£¨©Ā2£©£¨…ŤBCĶńĹ‚őŲ Ĺő™y=kx+b£¨‘Ú
x©Ā2=0£¨Ĺ‚Ķ√£ļx1=©Ā2£¨x2=4£¨ĶĪx=0 Ī£¨y=©Ā2£¨°ŗB£®4£¨0£©£¨C£®0£¨©Ā2£©£¨…ŤBCĶńĹ‚őŲ Ĺő™y=kx+b£¨‘Ú ![]() £¨Ĺ‚Ķ√£ļ
£¨Ĺ‚Ķ√£ļ 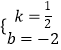 £¨°ŗy=
£¨°ŗy= ![]() x©Ā2£¨
x©Ā2£¨
…ŤD£®m£¨0£©£¨
°ŖDP°őy÷Š£¨
°ŗE£®m£¨ ![]() m©Ā2£©£¨P£®m£¨
m©Ā2£©£¨P£®m£¨ ![]() m2©Ā
m2©Ā ![]() m©Ā2£©£¨
m©Ā2£©£¨
°ŖOD=4PE£¨
°ŗm=4£® ![]() m2©Ā
m2©Ā ![]() m©Ā2©Ā
m©Ā2©Ā ![]() m+2£©£¨
m+2£©£¨
°ŗm=5£¨m=0£®…Š»•£©£¨
°ŗD£®5£¨0£©£¨P£®5£¨ ![]() £©£¨E£®5£¨
£©£¨E£®5£¨ ![]() £©£¨
£©£¨
°ŗňńĪŖ–őPOBEĶń√śĽż=S°ųOPD©ĀS°ųEBD= ![]() °Ń5°Ń
°Ń5°Ń ![]() ©Ā
©Ā ![]() 1°Ń
1°Ń ![]() =
= ![]() £Ľ
£Ľ
£®3£©
Ĺ‚£ļīś‘ŕ£¨…ŤM£®n£¨ ![]() n©Ā2£©£¨
n©Ā2£©£¨
ĘŔ“‘BDő™∂‘Ĺ«ŌŖ£¨»ÁÕľ1£¨
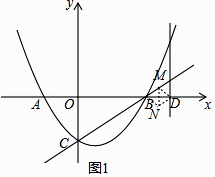
°ŖňńĪŖ–őBNDM «Ń‚–ő£¨
°ŗMNīĻ÷Ī∆Ĺ∑÷BD£¨
°ŗn=4+ ![]() £¨
£¨
°ŗM£® ![]() £¨
£¨ ![]() £©£¨
£©£¨
°ŖM£¨NĻō”ŕx÷Š∂‘≥∆£¨
°ŗN£® ![]() £¨©Ā
£¨©Ā ![]() £©£Ľ
£©£Ľ
Ęŕ“‘BDő™ĪŖ£¨»ÁÕľ2£¨
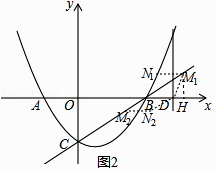
°ŖňńĪŖ–őBNDM «Ń‚–ő£¨
°ŗMN°őBD£¨MN=BD=MD=1£¨
ĻżM◊ųMH°Õx÷Š”ŕH£¨
°ŗMH2+DH2=DM2£¨
ľī£® ![]() n©Ā2£©2+£®n©Ā5£©2=12£¨
n©Ā2£©2+£®n©Ā5£©2=12£¨
°ŗn1=4£®≤ĽļŌŐ‚“‚£©£¨n2=5.6£¨
°ŗN£®4.6£¨ ![]() £©£¨
£©£¨
Õ¨ņŪ£® ![]() n©Ā2£©2+£®4©Ān£©2=1£¨
n©Ā2£©2+£®4©Ān£©2=1£¨
°ŗn1=4+ ![]() £®≤ĽļŌŐ‚“‚£¨…Š»•£©£¨n2=4©Ā
£®≤ĽļŌŐ‚“‚£¨…Š»•£©£¨n2=4©Ā ![]() £¨
£¨
°ŗN£®5©Ā ![]() £¨
£¨ ![]() £©£¨
£©£¨
ĘŘ“‘BDő™ĪŖ£¨»ÁÕľ3£¨

ĻżM◊ųMH°Õx÷Š”ŕH£¨
°ŗMH2+BH2=BM2£¨
ľī£® ![]() n©Ā2£©2+£®n©Ā4£©2=12£¨
n©Ā2£©2+£®n©Ā4£©2=12£¨
°ŗn1=4+ ![]() £¨n2=4©Ā
£¨n2=4©Ā ![]() £®≤ĽļŌŐ‚“‚£¨…Š»•£©£¨
£®≤ĽļŌŐ‚“‚£¨…Š»•£©£¨
°ŗN£®5+ ![]() £¨
£¨ ![]() £©£¨
£©£¨
◊Ř…Ōňý Ų£¨ĶĪN£® ![]() £¨©Ā
£¨©Ā ![]() £©ĽÚ£®4.6£¨
£©ĽÚ£®4.6£¨ ![]() £©ĽÚ£®5©Ā
£©ĽÚ£®5©Ā ![]() £¨
£¨ ![]() £©ĽÚ£®5+
£©ĽÚ£®5+ ![]() £¨
£¨ ![]() £©£¨“‘Ķ„B£¨D£¨M£¨Nő™∂•Ķ„ĶńňńĪŖ–ő «Ń‚–ő£ģ
£©£¨“‘Ķ„B£¨D£¨M£¨Nő™∂•Ķ„ĶńňńĪŖ–ő «Ń‚–ő£ģ
°ĺĹ‚őŲ°Ņ£®1£©”…Ň◊őÔŌŖy=ax2+bx©Ā2Ķń∂‘≥∆÷Š «÷ĪŌŖx=1£¨A£®©Ā2£¨0£©‘ŕŇ◊őÔŌŖ…Ō£¨”ŕ «Ń–∑Ĺ≥ŐľīŅ…Ķ√ĶĹĹŠ¬Ř£Ľ£®2£©łýĺ›ļĮ żĹ‚őŲ ĹĶ√ĶĹB£®4£¨0£©£¨C£®0£¨©Ā2£©£¨«ůĶ√BCĶńĹ‚őŲ Ĺő™y= ![]() x©Ā2£¨…ŤD£®m£¨0£©£¨Ķ√ĶĹE£®m£¨
x©Ā2£¨…ŤD£®m£¨0£©£¨Ķ√ĶĹE£®m£¨ ![]() m©Ā2£©£¨P£®m£¨
m©Ā2£©£¨P£®m£¨ ![]() m2©Ā
m2©Ā ![]() m©Ā2£©£¨łý囓—÷™ŐűľĢŃ–∑Ĺ≥ŐĶ√ĶĹm=5£¨m=0£®…Š»•£©£¨«ůĶ√D£®5£¨0£©£¨P£®5£¨
m©Ā2£©£¨łý囓—÷™ŐűľĢŃ–∑Ĺ≥ŐĶ√ĶĹm=5£¨m=0£®…Š»•£©£¨«ůĶ√D£®5£¨0£©£¨P£®5£¨ ![]() £©£¨E£®5£¨
£©£¨E£®5£¨ ![]() £©£¨łýĺ›»żĹ«–őĶń√śĽżĻę ĹľīŅ…Ķ√ĶĹĹŠ¬Ř£Ľ£®3£©…ŤM£®n£¨
£©£¨łýĺ›»żĹ«–őĶń√śĽżĻę ĹľīŅ…Ķ√ĶĹĹŠ¬Ř£Ľ£®3£©…ŤM£®n£¨ ![]() n©Ā2£©£¨ĘŔ“‘BDő™∂‘Ĺ«ŌŖ£¨łýĺ›Ń‚–őĶń–‘÷ Ķ√ĶĹMNīĻ÷Ī∆Ĺ∑÷BD£¨«ůĶ√n=4+
n©Ā2£©£¨ĘŔ“‘BDő™∂‘Ĺ«ŌŖ£¨łýĺ›Ń‚–őĶń–‘÷ Ķ√ĶĹMNīĻ÷Ī∆Ĺ∑÷BD£¨«ůĶ√n=4+ ![]() £¨”ŕ «Ķ√ĶĹN£®
£¨”ŕ «Ķ√ĶĹN£® ![]() £¨©Ā
£¨©Ā ![]() £©£ĽĘŕ“‘BDő™ĪŖ£¨łýĺ›Ń‚–őĶń–‘÷ Ķ√ĶĹMN°őBD£¨MN=BD=MD=1£¨ĻżM◊ųMH°Õx÷Š”ŕH£¨łýĺ›ĻīĻ…∂®ņŪŃ–∑Ĺ≥ŐľīŅ…Ķ√ĶĹĹŠ¬Ř£ģ
£©£ĽĘŕ“‘BDő™ĪŖ£¨łýĺ›Ń‚–őĶń–‘÷ Ķ√ĶĹMN°őBD£¨MN=BD=MD=1£¨ĻżM◊ųMH°Õx÷Š”ŕH£¨łýĺ›ĻīĻ…∂®ņŪŃ–∑Ĺ≥ŐľīŅ…Ķ√ĶĹĹŠ¬Ř£ģ


 –¬ŅőĪÍĹ◊Ő›‘ń∂Ń—ĶŃ∑ŌĶŃ–īūįł
–¬ŅőĪÍĹ◊Ő›‘ń∂Ń—ĶŃ∑ŌĶŃ–īūįł
| ńÍľ∂ | łŖ÷–Ņő≥Ő | ńÍľ∂ | ≥ű÷–Ņő≥Ő |
| łŖ“Ľ | łŖ“Ľ√‚∑—Ņő≥ŐÕ∆ľŲ£° | ≥ű“Ľ | ≥ű“Ľ√‚∑—Ņő≥ŐÕ∆ľŲ£° |
| łŖ∂Ģ | łŖ∂Ģ√‚∑—Ņő≥ŐÕ∆ľŲ£° | ≥ű∂Ģ | ≥ű∂Ģ√‚∑—Ņő≥ŐÕ∆ľŲ£° |
| łŖ»ż | łŖ»ż√‚∑—Ņő≥ŐÕ∆ľŲ£° | ≥ű»ż | ≥ű»ż√‚∑—Ņő≥ŐÕ∆ľŲ£° |
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ»ÁÕľĘŔ£¨Ķ„O «÷ĪŌŖAB…ŌĶń“ĽĶ„£¨°ŌCOD «÷ĪĹ«£¨OE∆Ĺ∑÷°ŌBOC£ģ
(1)»ÁÕľĘŔ£¨»Ű°ŌAOC=40°„£¨«ů°ŌDOEĶń∂» ż£Ľ
(2)»ÁÕľĘŔ£¨»Ű°ŌAOC=¶Ń£¨÷ĪĹ”–ī≥Ų°ŌDOEĶń∂» ż£®”√ļ¨¶ŃĶńīķ ż ĹĪŪ ĺ£©
(3)ĹęÕľĘŔ÷–Ķń°ŌCOD»∆∂•Ķ„Oň≥ Ī’Ž–ż◊™÷ŃÕľĘŕĶńőĽ÷√£¨OE∆Ĺ∑÷°ŌBOC£ģ
ĘŔŐĹĺŅ°ŌAOCļÕ°ŌDOEĶń∂» ż÷ģľšĶńĻōŌĶ£¨–ī≥Ųń„ĶńĹŠ¬Ř£¨≤ĘňĶ√ųņŪ”…£Ľ
Ęŕ‘ŕ°ŌAOCĶńńŕ≤Ņ”–“ĽŐű…šŌŖOF£¨«“°ŌAOC©Ā3°ŌAOF=2°ŌBOE£¨ ‘»∑∂®°ŌAOF”Ž°ŌDOEĶń∂» ż÷ģľšĶńĻōŌĶ£¨ňĶ√ųņŪ”…£ģ
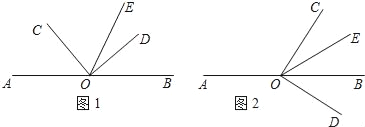
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°ŅŌ»ĽĮľÚ£¨‘Ŕ«ů÷Ķ£ļ£® ![]() ©Ā
©Ā ![]() £©°¬£®1©Ā
£©°¬£®1©Ā ![]() £©£¨∆š÷–x=£®
£©£¨∆š÷–x=£® ![]() £©©Ā1©Ā£®2017©Ā
£©©Ā1©Ā£®2017©Ā ![]() £©0 £¨ y=
£©0 £¨ y= ![]() sin60°„£ģ
sin60°„£ģ
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ“Ľį„«ťŅŲŌ¬![]() ≤Ľ≥…ŃĘ£¨Ķę”––© żŅ…“‘ ĻĶ√ňŁ≥…ŃĘ£¨ņż»Á£ļm=n=0 Ī£¨ő“√«≥∆ ĻĶ√
≤Ľ≥…ŃĘ£¨Ķę”––© żŅ…“‘ ĻĶ√ňŁ≥…ŃĘ£¨ņż»Á£ļm=n=0 Ī£¨ő“√«≥∆ ĻĶ√![]() ≥…ŃĘĶń“Ľ∂‘ żm£¨nő™°įŌŗįť ż∂‘°Ī£¨ľ«ő™£®m£¨n£©£ģ
≥…ŃĘĶń“Ľ∂‘ żm£¨nő™°įŌŗįť ż∂‘°Ī£¨ľ«ő™£®m£¨n£©£ģ
£®1£©»Ű£®m£¨1£© «°įŌŗįť ż∂‘°Ī£¨‘Úm=_____£Ľ
£®2£©£®m£¨n£© «°įŌŗįť ż∂‘°Ī£¨‘Úīķ ż Ĺ![]() m©Ā[n+
m©Ā[n+![]() £®6©Ā12n©Ā15m£©]Ķń÷Ķő™_____£ģ
£®6©Ā12n©Ā15m£©]Ķń÷Ķő™_____£ģ
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ»ÁÕľ£¨‘ŕ∆Ĺ√ś÷ĪĹ«◊ÝĪÍŌĶ÷–£¨÷ĪŌŖy1=x+1”Žňę«ķŌŖ![]() £®k£ĺ0£©ŌŗĹĽ”ŕĶ„A°ĘB£¨“—÷™Ķ„A◊ÝĪÍ£®2£¨m£©.
£®k£ĺ0£©ŌŗĹĽ”ŕĶ„A°ĘB£¨“—÷™Ķ„A◊ÝĪÍ£®2£¨m£©.
£®1£©«ůkĶń÷Ķ£Ľ
£®2£©«ůĶ„BĶń◊ÝĪÍ£¨≤ĘĻŘ≤žÕľŌů£¨–ī≥ŲĶĪ![]() Ī£¨xĶń»°÷Ķ∑∂őß.
Ī£¨xĶń»°÷Ķ∑∂őß.

≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ»ÁÕľ£¨Ň◊őÔŌŖy=©Āx2+bx+c£®a°Ŕ0£©”Žx÷ŠĹĽ”ŕĶ„A£®©Ā1£¨0£©ļÕB£®3£¨0£©£¨”Žy÷ŠĹĽ”ŕĶ„C£¨Ķ„DĶńļŠ◊ÝĪÍő™m£®0£ľm£ľ3£©£¨Ń¨ĹŠDC≤Ę—”≥§÷ŃE£¨ ĻĶ√CE=CD£¨Ń¨ĹŠBE£¨BC£ģ
£®1£©«ůŇ◊őÔŌŖĶńĹ‚őŲ Ĺ£Ľ
£®2£©”√ļ¨mĶńīķ ż ĹĪŪ ĺĶ„EĶń◊ÝĪÍ£¨≤Ę«ů≥ŲĶ„E◊›◊ÝĪÍĶń∑∂őߣĽ
£®3£©«ů°ųBCEĶń√śĽż◊Óīů÷Ķ£ģ

≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ»ÁÕľ£¨”√Ľū≤ŮįŰįŕ≥Ų“ĽŃ–’ż∑Ĺ–őÕľįł£¨ĶŕĘŔłŲÕľįł”√Ńň 4 łý£¨ĶŕĘŕłŲÕľįł”√Ńň 12 łý£¨ĶŕĘŘłŲÕľįł”√Ńň 24 łý£¨įī’’’‚÷÷∑Ĺ ĹįŕŌ¬»•£¨įŕ≥ŲĶŕĘřłŲÕľįł”√Ľū≤ŮįŰĶńłý ż «£® £©

A. 84 B. 81 C. 78 D. 76
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ»ÁÕľ£ļĺō–őABCD÷–£¨AB=2£¨BC=5£¨E°ĘP∑÷Īū‘ŕAD°ĘBC…Ō£¨«“DE=BP=1£ģ

£®1£©Ň–∂Ō°ųBECĶń–ő◊ī£¨≤ĘňĶ√ųņŪ”…£Ņ
£®2£©Ň–∂ŌňńĪŖ–őEFPH « ≤√īŐō ‚ňńĪŖ–ő£Ņ≤Ę÷§√ųń„ĶńŇ–∂Ō£Ľ
£®3£©«ůňńĪŖ–őEFPHĶń√śĽż£ģ
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
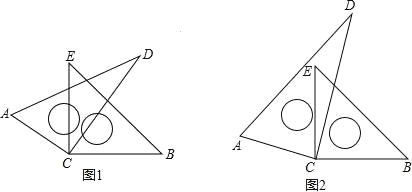
°ĺŐ‚ńŅ°Ņ»ÁÕľ£¨Ĺę“ĽłĪ÷ĪĹ«»żĹ«≥ŖĶń÷ĪĹ«∂•Ķ„CĶĢ∑Ň‘ŕ“Ľ∆ū£ģ
£®1£©»ÁÕľ 1£¨»Ű CE «°ļ√ «°ŌACD ĶńĹ«∆Ĺ∑÷ŌŖ£¨«Žń„≤¬ŌŽīň Ī CD «≤Ľ «°ŌECB ĶńĹ«∆Ĺ∑÷ŌŖ£Ņ÷ĽĽōīū≥Ų°į «°ĪĽÚ°į≤Ľ «°ĪľīŅ…£Ľ
£®2£©»ÁÕľ 2£¨»Ű°ŌECD=¶Ń£¨CD ‘ŕ°ŌBCE Ķńńŕ≤Ņ£¨«Žń„≤¬ŌŽ°ŌACE ”Ž°ŌDCB «∑ŮŌŗĶ»£Ņ≤ĘľÚ ŲņŪ”…£Ľ
£®3£©‘ŕ£®2£©ĶńŐűľĢŌ¬£¨«Žő °ŌECD ”Ž°ŌACB ĶńļÕ «∂ŗ…Ŕ£Ņ≤ĘľÚ ŲņŪ”…£ģ
≤ťŅīīūįłļÕĹ‚őŲ>>
Ļķľ —ß–£”Ň—° - Ń∑Ōį≤ŠŃ–ĪŪ - ‘Ő‚Ń–ĪŪ
ļĢĪĪ °Ľ•Ń™ÕÝő•∑®ļÕ≤ĽŃľ–ŇŌĘĺŔĪ®∆ĹŐ® | ÕÝ…Ō”–ļ¶–ŇŌĘĺŔĪ®◊®«Ý | ĶÁ–Ň’©∆≠ĺŔĪ®◊®«Ý | …śņķ ∑–ťőř÷ų“Ś”–ļ¶–ŇŌĘĺŔĪ®◊®«Ý | …ś∆ů«÷»®ĺŔĪ®◊®«Ý
ő•∑®ļÕ≤ĽŃľ–ŇŌĘĺŔĪ®ĶÁĽį£ļ027-86699610 ĺŔĪ®” Ōš£ļ58377363@163.com