
【题目】如图,在平面直角坐标系中,直线y1=x+1与双曲线![]() (k>0)相交于点A、B,已知点A坐标(2,m).
(k>0)相交于点A、B,已知点A坐标(2,m).
(1)求k的值;
(2)求点B的坐标,并观察图象,写出当![]() 时,x的取值范围.
时,x的取值范围.

【答案】(1)k=6;(2)当x<﹣3或0<x<2时,![]() ;
;
【解析】(1)设A(2,m),将A纵坐标代入一次函数解析式求出m的值,确定出A坐标,代入反比例解析式求出k的值,即可确定出反比例解析式;
(2)联立两函数解析式求出B的坐标,由A与B横坐标,利用图象即可求出当![]() 时,自变量x的取值范围.
时,自变量x的取值范围.
(1)∵A(2,m),
将A(2,m)代入直线y=x+1得:m=3,即A(2,3)
将A(2,3)代入关系式 y=![]() 得:k=6;
得:k=6;
(2)联立直线与反比例解析式得: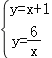 ,
,
消去y得: x+1=![]() ,
,
解得: x=2或x=﹣3,
将x=﹣3代入y=x+1, 得:y=﹣3+1=﹣2,即B(﹣3,﹣2),
则当x<﹣3或0<x<2时,![]() .
.


科目:初中数学 来源: 题型:
【题目】为了解学生参加户外活动的情况,和谐中学对学生每天参加户外活动的时间进行抽样调查,并将调查结果绘制成如图两幅不完整的统计图,根据图示,请回答下列问题:
(Ⅰ)被抽样调查的学生有 人,并补全条形统计图 ;
(Ⅱ)每天户外活动时间的中位数是 (小时);
(Ⅲ)该校共有2000名学生,请估计该校每天户外活动时间超过1小时的学生有 人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,![]() ,
,![]() 的平分线与BC的延长线交于点E,与DC交于点F,且点F为边DC的中点,
的平分线与BC的延长线交于点E,与DC交于点F,且点F为边DC的中点,![]() ,垂足为G,若
,垂足为G,若![]() ,则AE的边长为
,则AE的边长为![]()
![]()

A. ![]() B.
B. ![]() C. 4 D. 8
C. 4 D. 8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知数轴上点A表示的数为8,B是数轴上位于点A左侧一点,且AB=20,
(1)写出数轴上点B表示的数 ;
(2)|5﹣3|表示5与3之差的绝对值,实际上也可理解为5与3两数在数轴上所对的两点之间的距离.如|x﹣3|的几何意义是数轴上表示有理数x的点与表示有理数3的点之间的距离.试探索:
①:若|x﹣8|=2,则x= .
②:|x+12|+|x﹣8|的最小值为 .
(3)动点P从O点出发,以每秒5个单位长度的速度沿数轴向右匀速运动,设运动时间为t(t>0)秒.求当t为多少秒时?A,P两点之间的距离为2;
(4)动点P,Q分别从O,B两点,同时出发,点P以每秒5个单位长度沿数轴向右匀速运动,Q点以P点速度的两倍,沿数轴向右匀速运动,设运动时间为t(t>0)秒.问当t为多少秒时?P,Q之间的距离为4.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)计算:(﹣1)3÷(﹣5)2×(﹣![]() )﹣|0.8﹣1|;
)﹣|0.8﹣1|;
(2)计算:(1![]() +
+![]() ﹣2.75)×(﹣24)+(﹣1)2011﹣|﹣2|;
﹣2.75)×(﹣24)+(﹣1)2011﹣|﹣2|;
(3)先化简,再求值,已知|x+2|+(y﹣![]() )2=0,求3(x2﹣2xy)﹣[3x2﹣2y+2(xy+y)]的值.
)2=0,求3(x2﹣2xy)﹣[3x2﹣2y+2(xy+y)]的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx﹣2的对称轴是直线x=1,与x轴交于A,B两点,与y轴交于点C,点A的坐标为(﹣2,0),点P为抛物线上的一个动点,过点P作PD⊥x轴于点D,交直线BC于点E.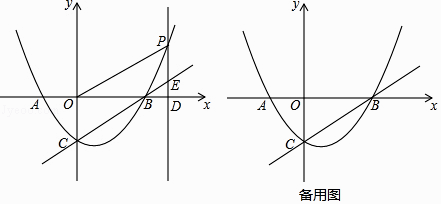
(1)求抛物线解析式;
(2)若点P在第一象限内,当OD=4PE时,求四边形POBE的面积;
(3)在(2)的条件下,若点M为直线BC上一点,点N为平面直角坐标系内一点,是否存在这样的点M和点N,使得以点B,D,M,N为顶点的四边形是菱形?若存在上,直接写出点N的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一副三角板中的两块直角三角尺的直角顶点 O 按如图方式叠放在一起.

( 1 ) 如图 1 , 若∠ BOD=35° , 则∠ AOC= ; 若∠AOC=135°, 则∠BOD= ;
(2)如图2,若∠AOC=140°,则∠BOD= ;
(3)猜想∠AOC 与∠BOD 的大小关系,并结合图1说明理由.
(4)三角尺 AOB 不动,将三角尺 COD 的 OD 边与 OA 边重合,然后绕点 O 按顺时针或逆时针方向任意转动一个角度,当∠A OD(0°<∠AOD<90°)等于多少度时,这两块三角尺各有一条边互相垂直,直接写出∠AOD 角度所有可能的值,不用说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】题目:在同一平面上,若∠AOB=75°,∠BOC=15°,求∠AOC的度数.
下面是七(2)班马小虎同学的解题过程:
解:根据题意画出图形,如图所示,
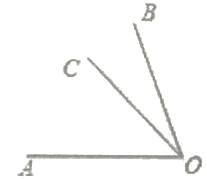
∵∠AOC=∠AOB-∠BOC=75°-75°=60°
∴∠AOC=60°
若你是老师,会判马小虎满分吗?若会,说明理由;若不会,请指出错误之处,并给出你认为正确的解法.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O是△ABC的外接圆,BC为⊙O的直径,点E为△ABC的内心,连接AE并延长交⊙O于D点,连接BD并延长至F,使得BD=DF,连接CF、BE. 
(1)求证:DB=DE;
(2)求证:直线CF为⊙O的切线
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com