
【题目】计算:
(1)计算:(﹣1)3÷(﹣5)2×(﹣![]() )﹣|0.8﹣1|;
)﹣|0.8﹣1|;
(2)计算:(1![]() +
+![]() ﹣2.75)×(﹣24)+(﹣1)2011﹣|﹣2|;
﹣2.75)×(﹣24)+(﹣1)2011﹣|﹣2|;
(3)先化简,再求值,已知|x+2|+(y﹣![]() )2=0,求3(x2﹣2xy)﹣[3x2﹣2y+2(xy+y)]的值.
)2=0,求3(x2﹣2xy)﹣[3x2﹣2y+2(xy+y)]的值.
【答案】(1)![]() ;(2)28;(3)8.
;(2)28;(3)8.
【解析】
(1)先计算乘方,绝对值,再计算乘除,最后加减得结果;(2)先计算乘方和绝对值,再运用乘法对加法的分配律,最后加减得结果;(3)利用非负数的性质,先确定x、y的值,再化简整式,最后代入求值.
(1)原式=﹣1÷25×(﹣![]() )﹣0.2
)﹣0.2
=1×![]() ×
×![]() ﹣
﹣![]()
=![]() ﹣
﹣![]()
=﹣![]() ;
;
(2)原式=(![]() +
+![]() ﹣
﹣![]() )×(﹣24)﹣1﹣2
)×(﹣24)﹣1﹣2
=﹣32﹣3+66﹣1﹣2
=28;
(3)∵|x+2|+(y﹣![]() )2=0,
)2=0,
又∵|x+2|≥0,(y﹣![]() )2≥0,
)2≥0,
∴x+2=0,y﹣![]() =0,
=0,
∴x=﹣2,y=![]() .
.
3(x2﹣2xy)﹣[3x2﹣2y+2(xy+y)]
=3x2﹣6xy﹣(3x2﹣2y+2xy+2y)
=3x2﹣6xy﹣3x2+2y﹣2xy﹣2y
=﹣8xy.
当x=﹣2,y=![]() 时,
时,
原式=﹣8×(﹣2)×![]()
=8.


科目:初中数学 来源: 题型:
【题目】课间休息时小明拿着两根木棒玩,小华看到后要小明给他玩,小明说:“较短木棒AB长40cm,较长木棒CD长60cm,将它们的一端重合,放在同一条直线上,此时两根木棒的中点分别是点E和点F,则点E和点F间的距离是多少?你说对了我就给你玩”聪明的你请帮小华求出此时两根木棒的中点E和F间的距离是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图A在数轴上所对应的数为﹣2.
(1)点B在点A右边距A点4个单位长度,求点B所对应的数;
(2)在(1)的条件下,点A以每秒2个单位长度沿数轴向左运动,点 B 以每秒2个单位长度沿数轴向右运动,当点A运动到﹣6所在的点处时,求A,B两点间距离.
(3)在(2)的条件下,现A点静止不动,B点再以每秒2个单位长度沿数轴向左运动时,经过多长时间A,B两点相距4个单位长度.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E在以AB为直径的⊙O上,点C是 ![]() 的中点,过点C作CD垂直于AE,交AE的延长线于点D,连接BE交AC于点F.
的中点,过点C作CD垂直于AE,交AE的延长线于点D,连接BE交AC于点F. 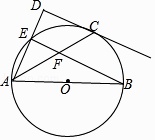
(1)求证:CD是⊙O的切线;
(2)若cos∠CAD= ![]() ,BF=15,求AC的长.
,BF=15,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线y1=x+1与双曲线![]() (k>0)相交于点A、B,已知点A坐标(2,m).
(k>0)相交于点A、B,已知点A坐标(2,m).
(1)求k的值;
(2)求点B的坐标,并观察图象,写出当![]() 时,x的取值范围.
时,x的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,将一点(横坐标与纵坐标不相等)的横坐标与纵坐标互换后得到的点叫这一点的“互换点”,如(﹣3,5)与(5,﹣3)是一对“互换点”.
(1)任意一对“互换点”能否都在一个反比例函数的图象上?为什么?
(2)M、N是一对“互换点”,若点M的坐标为(m,n),求直线MN的表达式(用含m、n的代数式表示);
(3)在抛物线y=x2+bx+c的图象上有一对“互换点”A、B,其中点A在反比例函数y=﹣ ![]() 的图象上,直线AB经过点P(
的图象上,直线AB经过点P( ![]() ,
, ![]() ),求此抛物线的表达式.
),求此抛物线的表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知凸五边形ABCDE的边长均相等,且∠DBE=∠ABE+∠CBD,AC=1,则BD必定满足( ) 
A.BD<2
B.BD=2
C.BD>2
D.以上情况均有可能
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com