
【题目】在平面直角坐标系中,将一点(横坐标与纵坐标不相等)的横坐标与纵坐标互换后得到的点叫这一点的“互换点”,如(﹣3,5)与(5,﹣3)是一对“互换点”.
(1)任意一对“互换点”能否都在一个反比例函数的图象上?为什么?
(2)M、N是一对“互换点”,若点M的坐标为(m,n),求直线MN的表达式(用含m、n的代数式表示);
(3)在抛物线y=x2+bx+c的图象上有一对“互换点”A、B,其中点A在反比例函数y=﹣ ![]() 的图象上,直线AB经过点P(
的图象上,直线AB经过点P( ![]() ,
, ![]() ),求此抛物线的表达式.
),求此抛物线的表达式.
【答案】
(1)解:不一定,
设这一对“互换点”的坐标为(a,b)和(b,a).
①当ab=0时,它们不可能在反比例函数的图象上,
②当ab≠0时,由 ![]() 可得
可得 ![]() ,即(a,b)和(b,a)都在反比例函数
,即(a,b)和(b,a)都在反比例函数 ![]() (k≠0)的图象上;
(k≠0)的图象上;
(2)解:由M(m,n)得N(n,m),设直线MN的表达式为y=cx+d(c≠0).
则有 ![]() 解得
解得 ![]() ,
,
∴直线MN的表达式为y=﹣x+m+n;
(3)解:设点A(p,q),则 ![]() ,
,
∵直线AB经过点P( ![]() ,
, ![]() ),由(2)得
),由(2)得 ![]() ,
,
∴p+q=1,
∴ ![]() ,
,
解并检验得:p=2或p=﹣1,
∴q=﹣1或q=2,
∴这一对“互换点”是(2,﹣1)和(﹣1,2),
将这一对“互换点”代入y=x2+bx+c得,
∴ ![]() 解得
解得 ![]() ,
,
∴此抛物线的表达式为y=x2﹣2x﹣1.
【解析】(1)设这一对“互换点”的坐标为(a,b)和(b,a).①当ab=0时,它们不可能在反比例函数的图象上,②当ab≠0时,由 ![]() 可得
可得 ![]() ,于是得到结论;(2)把M(m,n),N(n,m)代入y=cx+d,即可得到结论;(3)设点A(p,q),则
,于是得到结论;(2)把M(m,n),N(n,m)代入y=cx+d,即可得到结论;(3)设点A(p,q),则 ![]() ,由直线AB经过点P(
,由直线AB经过点P( ![]() ,
, ![]() ),得到p+q=1,得到q=﹣1或q=2,将这一对“互换点”代入y=x2+bx+c得,于是得到结论.
),得到p+q=1,得到q=﹣1或q=2,将这一对“互换点”代入y=x2+bx+c得,于是得到结论.
【考点精析】解答此题的关键在于理解确定一次函数的表达式的相关知识,掌握确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法.


科目:初中数学 来源: 题型:
【题目】历史上的数学巨人欧拉最先把关于x的多项式用记号f(x)来表示,例如f(x)=x2+3x﹣5,把x=某数时多项式的值用f(某数)来表示,例如x=1时多项式x2+3x﹣5的值记为f(1)=12+3×1﹣5=﹣1.
(1)已知g(x)=﹣2x2﹣3x+1,分别求出g(﹣1)和g(﹣2)的值.
(2)已知h(x)=ax3+2x2﹣x﹣14,![]() ,求a的值.
,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)计算:(﹣1)3÷(﹣5)2×(﹣![]() )﹣|0.8﹣1|;
)﹣|0.8﹣1|;
(2)计算:(1![]() +
+![]() ﹣2.75)×(﹣24)+(﹣1)2011﹣|﹣2|;
﹣2.75)×(﹣24)+(﹣1)2011﹣|﹣2|;
(3)先化简,再求值,已知|x+2|+(y﹣![]() )2=0,求3(x2﹣2xy)﹣[3x2﹣2y+2(xy+y)]的值.
)2=0,求3(x2﹣2xy)﹣[3x2﹣2y+2(xy+y)]的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一副三角板中的两块直角三角尺的直角顶点 O 按如图方式叠放在一起.

( 1 ) 如图 1 , 若∠ BOD=35° , 则∠ AOC= ; 若∠AOC=135°, 则∠BOD= ;
(2)如图2,若∠AOC=140°,则∠BOD= ;
(3)猜想∠AOC 与∠BOD 的大小关系,并结合图1说明理由.
(4)三角尺 AOB 不动,将三角尺 COD 的 OD 边与 OA 边重合,然后绕点 O 按顺时针或逆时针方向任意转动一个角度,当∠A OD(0°<∠AOD<90°)等于多少度时,这两块三角尺各有一条边互相垂直,直接写出∠AOD 角度所有可能的值,不用说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)5﹣(﹣3)+(﹣2)﹣1;
(2)2![]() ×(﹣
×(﹣![]() )÷(﹣3);
)÷(﹣3);
(3)﹣5×[1﹣(0.5+ ![]() )÷
)÷![]() ];
];
(4)20×(﹣![]() )+4×(﹣
)+4×(﹣![]() )+2×(﹣
)+2×(﹣![]() );
);
(5)﹣14-(![]() )÷(﹣
)÷(﹣![]() )×[﹣2﹣(﹣3)2]﹣(
)×[﹣2﹣(﹣3)2]﹣(![]() ﹣0.52).
﹣0.52).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】题目:在同一平面上,若∠AOB=75°,∠BOC=15°,求∠AOC的度数.
下面是七(2)班马小虎同学的解题过程:
解:根据题意画出图形,如图所示,
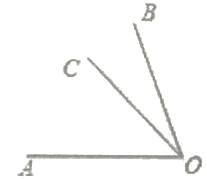
∵∠AOC=∠AOB-∠BOC=75°-75°=60°
∴∠AOC=60°
若你是老师,会判马小虎满分吗?若会,说明理由;若不会,请指出错误之处,并给出你认为正确的解法.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 的解析表达式为:y=-3x+3,且
的解析表达式为:y=-3x+3,且![]() 与x轴交于点D,直线
与x轴交于点D,直线![]() 经过点A,B,直线
经过点A,B,直线![]() ,
,![]() 交于点C.
交于点C.
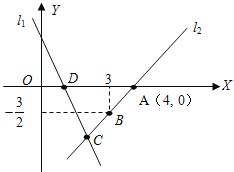
(1)求点D的坐标;
(2)求直线![]() 的解析表达式;
的解析表达式;
(3)求△ADC的面积;
(4)在直线![]() 上存在异于点C的另一点P,使得△ADP的面积是△ADC面积的2倍,请直接写出点P的坐标.
上存在异于点C的另一点P,使得△ADP的面积是△ADC面积的2倍,请直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程mx2+(3﹣m)x﹣3=0(m为实数,m≠0).
(1) 试说明:此方程总有两个实数根.
(2) 如果此方程的两个实数根都为正整数,求整数m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线EF交x,y轴子点F,E,交反比例函数![]() (x>0)图象于点C,D,OE=OF=
(x>0)图象于点C,D,OE=OF=![]() ,以CD为边作矩形ABCD,顶点A与B恰好落在y轴与x轴上.
,以CD为边作矩形ABCD,顶点A与B恰好落在y轴与x轴上.
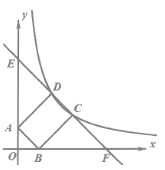
(1)若矩形ABCD是正方形,求CD的长;
(2)若AD:DC=2:1,求k的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com