
【题目】如图,直线![]() 的解析表达式为:y=-3x+3,且
的解析表达式为:y=-3x+3,且![]() 与x轴交于点D,直线
与x轴交于点D,直线![]() 经过点A,B,直线
经过点A,B,直线![]() ,
,![]() 交于点C.
交于点C.
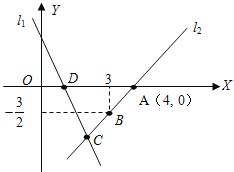
(1)求点D的坐标;
(2)求直线![]() 的解析表达式;
的解析表达式;
(3)求△ADC的面积;
(4)在直线![]() 上存在异于点C的另一点P,使得△ADP的面积是△ADC面积的2倍,请直接写出点P的坐标.
上存在异于点C的另一点P,使得△ADP的面积是△ADC面积的2倍,请直接写出点P的坐标.
【答案】(1)D(1,0);(2)![]() ;(3)
;(3)![]() ;(4)
;(4)![]() (8,6)或
(8,6)或![]() (0,-6).
(0,-6).
【解析】(1)已知l1的解析式,令y=0求出x的值即可;
(2)设l2的解析式为y=kx+b,由图联立方程组求出k,b的值;
(3)联立方程组,求出交点C的坐标,继而可求出S△ADC.
(4)△ADP与△ADC底边都是AD,面积为2倍,所以高为2倍,△ADC高就是点C到直线AD的距离的2倍,即C纵坐标的绝对值=6,则P到AD距离=6,得到点P纵坐标是![]() ,代入y=1.5x-6,y=6,得到x的值,从而得到结论.
,代入y=1.5x-6,y=6,得到x的值,从而得到结论.
(1)由y=﹣3x+3,令y=0,得﹣3x+3=0,∴x=1,∴D(1,0);
(2)设直线l2的解析表达式为y=kx+b,由图象知:x=4,y=0;
x=3,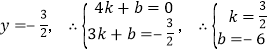 ,∴直线l2的解析表达式为
,∴直线l2的解析表达式为 ![]() ;
;
(3)由 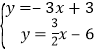 ,解得:
,解得: ![]() ,∴C(2,﹣3).
,∴C(2,﹣3).
∵AD=3,∴S△ADC=![]() ×3×|﹣3|=
×3×|﹣3|=![]() .
.
(4)△ADP与△ADC底边都是AD,面积为2倍,所以高为2倍,△ADC高就是点C到直线AD的距离的2倍,即C纵坐标的绝对值=6,则P到AD距离=6,∴点P纵坐标是![]() .
.
∵y=1.5x-6,y=6,∴1.5x-6=6, x=8,所以![]() (8,6).
(8,6).
∵y=1.5x-6,y=-6,∴1.5x-6=-6, x=0,所以![]() (0,-6)
(0,-6)
所以![]() (8,6)或
(8,6)或![]() (0,-6).
(0,-6).


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,将一点(横坐标与纵坐标不相等)的横坐标与纵坐标互换后得到的点叫这一点的“互换点”,如(﹣3,5)与(5,﹣3)是一对“互换点”.
(1)任意一对“互换点”能否都在一个反比例函数的图象上?为什么?
(2)M、N是一对“互换点”,若点M的坐标为(m,n),求直线MN的表达式(用含m、n的代数式表示);
(3)在抛物线y=x2+bx+c的图象上有一对“互换点”A、B,其中点A在反比例函数y=﹣ ![]() 的图象上,直线AB经过点P(
的图象上,直线AB经过点P( ![]() ,
, ![]() ),求此抛物线的表达式.
),求此抛物线的表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形纸片ABCD中,AB=2,∠A=60°,将菱形纸片翻折,使点A落在CD的中点E处,折痕为FG,点F,G分别在边AB,AD上,则EF的长为

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从共享单车,共享汽车等共享出行到共享雨伞等共享物品,各式各样的共享
经济模式在各个领域迅速的普及。
(1) 为获得泰州市市民参与共享经济的活动信息,下列调查方式中比较合理的是 ;
A.对某学校的全体同学进行问卷调查 B.对某小区的住户进行问卷调查
C.在全市里的不同区县,选取部分市民进行问卷调查
(2) 调查小组随机调查了泰兴市市民骑共享单车情况,某社区年龄在12~36岁的人有1000人,从中随机抽取了100人,统计了他们骑共享单车的人数,并绘制了如下不完整的统计图表.

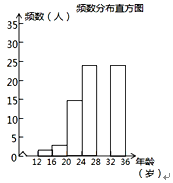
根据以上信息解答下列问题:
① 求出统计表中的a、b,并补全频数分布直方图
② 试估计这个社区年龄在20岁到32岁(含20岁,不含32岁)骑共享单车的人有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知凸五边形ABCDE的边长均相等,且∠DBE=∠ABE+∠CBD,AC=1,则BD必定满足( ) 
A.BD<2
B.BD=2
C.BD>2
D.以上情况均有可能
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直角坐标系xOy中,A(0,5),直线x=﹣5与x轴交于点D,直线y=﹣ ![]() x﹣
x﹣ ![]() 与x轴及直线x=﹣5分别交于点C,E,点B,E关于x轴对称,连接AB.
与x轴及直线x=﹣5分别交于点C,E,点B,E关于x轴对称,连接AB.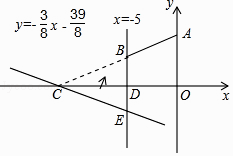
(1)求点C,E的坐标及直线AB的解析式;
(2)设面积的和S=S△CDE+S四边形ABDO , 求S的值;
(3)在求(2)中S时,嘉琪有个想法:“将△CDE沿x轴翻折到△CDB的位置,而△CDB与四边形ABDO拼接后可看成△AOC,这样求S便转化为直接求△AOC的面积不更快捷吗?”但大家经反复演算,发现S△AOC≠S,请通过计算解释他的想法错在哪里.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com