
【题目】如图,直角坐标系xOy中,A(0,5),直线x=﹣5与x轴交于点D,直线y=﹣ ![]() x﹣
x﹣ ![]() 与x轴及直线x=﹣5分别交于点C,E,点B,E关于x轴对称,连接AB.
与x轴及直线x=﹣5分别交于点C,E,点B,E关于x轴对称,连接AB.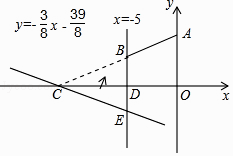
(1)求点C,E的坐标及直线AB的解析式;
(2)设面积的和S=S△CDE+S四边形ABDO , 求S的值;
(3)在求(2)中S时,嘉琪有个想法:“将△CDE沿x轴翻折到△CDB的位置,而△CDB与四边形ABDO拼接后可看成△AOC,这样求S便转化为直接求△AOC的面积不更快捷吗?”但大家经反复演算,发现S△AOC≠S,请通过计算解释他的想法错在哪里.
【答案】
(1)
解:在直线y=﹣ ![]() x﹣
x﹣ ![]() 中,
中,
令y=0,则有0=﹣ ![]() x﹣
x﹣ ![]() ,
,
∴x=﹣13,
∴C(﹣13,0),
令x=﹣5,则有y=﹣ ![]() ×(﹣5)﹣
×(﹣5)﹣ ![]() =﹣3,
=﹣3,
∴E(﹣5,﹣3),
∵点B,E关于x轴对称,
∴B(﹣5,3),
∵A(0,5),
∴设直线AB的解析式为y=kx+5,
∴﹣5k+5=3,
∴k= ![]() ,
,
∴直线AB的解析式为y= ![]() x+5
x+5
(2)
解:由(1)知,E(﹣5,﹣3),
∴DE=3,
∵C(﹣13,0),
∴CD=﹣5﹣(﹣13)=8,
∴S△CDE= ![]() CD×DE=12,
CD×DE=12,
由题意知,OA=5,OD=5,BD=3,
∴S四边形ABDO= ![]() (BD+OA)×OD=20,
(BD+OA)×OD=20,
∴S=S△CDE+S四边形ABDO=12+20=32
(3)
解:由(2)知,S=32,
在△AOC中,OA=5,OC=13,
∴S△AOC= ![]() OA×OC=
OA×OC= ![]() =32.5,
=32.5,
∴S≠S△AOC,
理由:由(1)知,直线AB的解析式为y= ![]() x+5,
x+5,
令y=0,则0= ![]() x+5,
x+5,
∴x=﹣ ![]() ≠﹣13,
≠﹣13,
∴点C不在直线AB上,
即:点A,B,C不在同一条直线上,
∴S△AOC≠S
【解析】(1)利用坐标轴上点的特点确定出点C的坐标,再利用直线的交点坐标的确定方法求出点E坐标,进而得到点B坐标,最后用待定系数法求出直线AB解析式;(2)直接利用直角三角形的面积计算方法和直角梯形的面积的计算即可得出结论,(3)先求出直线AB与x轴的交点坐标,判断出点C不在直线AB上,即可.
【考点精析】认真审题,首先需要了解一次函数的性质(一般地,一次函数y=kx+b有下列性质:(1)当k>0时,y随x的增大而增大(2)当k<0时,y随x的增大而减小).


科目:初中数学 来源: 题型:
【题目】如图,直线![]() 的解析表达式为:y=-3x+3,且
的解析表达式为:y=-3x+3,且![]() 与x轴交于点D,直线
与x轴交于点D,直线![]() 经过点A,B,直线
经过点A,B,直线![]() ,
,![]() 交于点C.
交于点C.
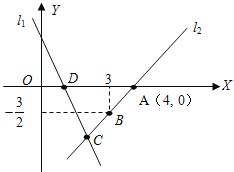
(1)求点D的坐标;
(2)求直线![]() 的解析表达式;
的解析表达式;
(3)求△ADC的面积;
(4)在直线![]() 上存在异于点C的另一点P,使得△ADP的面积是△ADC面积的2倍,请直接写出点P的坐标.
上存在异于点C的另一点P,使得△ADP的面积是△ADC面积的2倍,请直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在现实生活中,我们会看到许多“标准”的矩形,如我们的课本封面、A4的打印纸等,其实这些矩形的长与宽之比都为 ![]() :1,我们不妨就把这样的矩形称为“标准矩形”,在“标准矩形”ABCD中,P为DC边上一定点,且CP=BC,如图所示.
:1,我们不妨就把这样的矩形称为“标准矩形”,在“标准矩形”ABCD中,P为DC边上一定点,且CP=BC,如图所示.
(1)如图①,求证:BA=BP;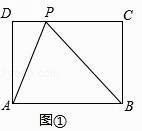
(2)如图②,点Q在DC上,且DQ=CP,若G为BC边上一动点,当△AGQ的周长最小时,求 ![]() 的值;
的值;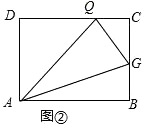
(3)如图③,已知AD=1,在(2)的条件下,连接AG并延长交DC的延长线于点F,连接BF,T为BF的中点,M、N分别为线段PF与AB上的动点,且始终保持PM=BN,请证明:△MNT的面积S为定值,并求出这个定值.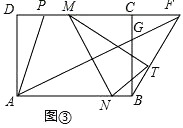
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线EF交x,y轴子点F,E,交反比例函数![]() (x>0)图象于点C,D,OE=OF=
(x>0)图象于点C,D,OE=OF=![]() ,以CD为边作矩形ABCD,顶点A与B恰好落在y轴与x轴上.
,以CD为边作矩形ABCD,顶点A与B恰好落在y轴与x轴上.
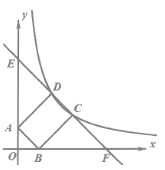
(1)若矩形ABCD是正方形,求CD的长;
(2)若AD:DC=2:1,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一条不完整的数轴上从左到右有点A,B,C,其中AB=2,BC=1,如图所示,设点A,B,C所对应数的和是p. ![]()
(1)若以B为原点,写出点A,C所对应的数,并计算p的值;若以C为原点,p又是多少?
(2)若原点O在图中数轴上点C的右边,且CO=28,求p.
查看答案和解析>>
科目:初中数学 来源: 题型:
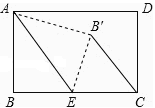
【题目】现有一张矩形纸片ABCD(如图),其中AB=4cm,BC=6cm,点E是BC的中点.将纸片沿直线AE折叠,点B落在四边形AECD内,记为点B′.则线段B′C= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点C为线段AB上一点,AC=8cm,CB=6cm,点M、N分别是AC、BC的中点.
(1)求线段MN的长;
(2)若AC+BC=acm,其他条件不变,直接写出线段MN的长为 .
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
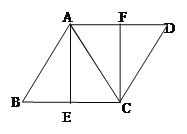
【题目】如图,已知菱形ABCD,AB=AC,E、F分别是BC、AD的中点,连接AE、CF
(1)填空∠B=_______°;
(2)求证:四边形AECF是矩形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=kx+6分别与x轴、y轴交于点E,F,已知点E的坐标为(-8,0),点A的坐标为(-6,0).
(1)求k的值;
(2)若点P(x,y)是该直线上的一个动点,探究:当△OPA的面积为27时,求点P的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com