
【题目】在现实生活中,我们会看到许多“标准”的矩形,如我们的课本封面、A4的打印纸等,其实这些矩形的长与宽之比都为 ![]() :1,我们不妨就把这样的矩形称为“标准矩形”,在“标准矩形”ABCD中,P为DC边上一定点,且CP=BC,如图所示.
:1,我们不妨就把这样的矩形称为“标准矩形”,在“标准矩形”ABCD中,P为DC边上一定点,且CP=BC,如图所示.
(1)如图①,求证:BA=BP;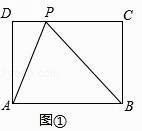
(2)如图②,点Q在DC上,且DQ=CP,若G为BC边上一动点,当△AGQ的周长最小时,求 ![]() 的值;
的值;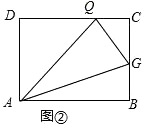
(3)如图③,已知AD=1,在(2)的条件下,连接AG并延长交DC的延长线于点F,连接BF,T为BF的中点,M、N分别为线段PF与AB上的动点,且始终保持PM=BN,请证明:△MNT的面积S为定值,并求出这个定值.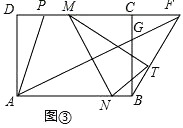
【答案】
(1)
证明:如图①中,设AD=BC=a,则AB=CD= ![]() a.
a.

∵四边形ABCD是矩形,
∴∠C=90°,
∵PC=AD=BC=a,
∴PB= ![]() =
= ![]() a,
a,
∴BA=BP
(2)
解:如图②中,作Q关于BC的对称点Q′,连接AQ′交BC于G,此时△AQG的周长最小.
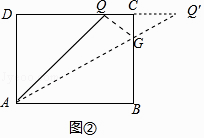
设AD=BC=QD=a,则AB=CD= ![]() a,
a,
∴CQ=CQ′= ![]() a﹣a,
a﹣a,
∵CQ′//AB,
∴ ![]() =
= ![]() =
= ![]() =
= ![]()
(3)
证明:如图③中,作TH//AB交NM于H,交BC于K.
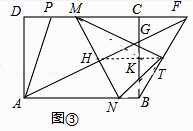
由(2)可知,AD=BC=1,AB=CD= ![]() ,DP=CF=
,DP=CF= ![]() ﹣1,
﹣1,
∵S△MNT= ![]() THCK+
THCK+ ![]() THBK=
THBK= ![]() HT(KC+KB)=
HT(KC+KB)= ![]() HTBC=
HTBC= ![]() HT,
HT,
∵TH//AB//FM,TF=TB,
∴HM=HN,
∴HT= ![]() (FM+BN),
(FM+BN),
∵BN=PM,
∴HT= ![]() (FM+PM)=
(FM+PM)= ![]() PF=
PF= ![]() (1+
(1+ ![]() ﹣1)=
﹣1)= ![]() ,
,
∴S△MNT= ![]() HT=
HT= ![]() =定值
=定值
【解析】(1)如图①中,设AD=BC=a,则AB=CD= ![]() a.通过计算得出AB=BP=
a.通过计算得出AB=BP= ![]() a,由此即可证明;(2)如图②中,作Q关于BC的对称点Q′,连接AQ′交BC于G,此时△AQG的周长最小.设AD=BC=QD=a,则AB=CD=
a,由此即可证明;(2)如图②中,作Q关于BC的对称点Q′,连接AQ′交BC于G,此时△AQG的周长最小.设AD=BC=QD=a,则AB=CD= ![]() a,可得CQ=CQ′=
a,可得CQ=CQ′= ![]() a﹣a,由CQ′//AB,推出
a﹣a,由CQ′//AB,推出 ![]() =
= ![]() =
= ![]() =
= ![]() ;(3)如图③中,作TH//AB交NM于H,交BC于K.由S△MNT=
;(3)如图③中,作TH//AB交NM于H,交BC于K.由S△MNT= ![]() THCK+
THCK+ ![]() THBK=
THBK= ![]() HT(KC+KB)=
HT(KC+KB)= ![]() HTBC=
HTBC= ![]() HT,利用梯形的中位线定理求出HT即可解决问题;
HT,利用梯形的中位线定理求出HT即可解决问题;


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】从共享单车,共享汽车等共享出行到共享雨伞等共享物品,各式各样的共享
经济模式在各个领域迅速的普及。
(1) 为获得泰州市市民参与共享经济的活动信息,下列调查方式中比较合理的是 ;
A.对某学校的全体同学进行问卷调查 B.对某小区的住户进行问卷调查
C.在全市里的不同区县,选取部分市民进行问卷调查
(2) 调查小组随机调查了泰兴市市民骑共享单车情况,某社区年龄在12~36岁的人有1000人,从中随机抽取了100人,统计了他们骑共享单车的人数,并绘制了如下不完整的统计图表.

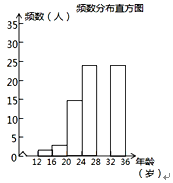
根据以上信息解答下列问题:
① 求出统计表中的a、b,并补全频数分布直方图
② 试估计这个社区年龄在20岁到32岁(含20岁,不含32岁)骑共享单车的人有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知凸五边形ABCDE的边长均相等,且∠DBE=∠ABE+∠CBD,AC=1,则BD必定满足( ) 
A.BD<2
B.BD=2
C.BD>2
D.以上情况均有可能
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】北京地铁1号线是中国最早的地铁线路,2000年实现了23个车站的贯通运营,该线西起苹果园站,东至四惠东站,全长约31千米.下表是北京地铁1号线首末车时刻表,开往四惠东方向和苹果园方向的首车的平均速度均为每小时60千米,求由苹果园站和四惠东站开出的首车第一次相遇的时间.
北京地铁1号线首末车时刻表 | ||||
车站名称 | 往四惠东方向 | 往苹果园方向 | ||
首车时间 | 末车时间 | 首车时间 | 末车时间 | |
苹果园 | 5:10 | 22:55 | -- | -- |
… | … | … | … | … |
四惠东 | -- | -- | 5:05 | 23:15 |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将连续的奇数1、3、5、7、9,……排成如下的数表:

(1)十字框中的5个数的和与中间的数23有什么关系?若将十字框上下左右平移,可框住另外5个数,这5个数还有这种规律吗?
(2)设十字框中中间的数为a,用含a的式子表示十字框中的其他四个数;
(3)十字框中的5个数的和能等于2018吗?若能,请写出这5个数;若不能,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解方程![]() ﹣1的步骤如下:
﹣1的步骤如下:
(解析)第一步:![]() ﹣1(分数的基本性质)
﹣1(分数的基本性质)
第二步:2x﹣1=3(2x+8)﹣3……(①)
第三步:2x﹣1=6x+24﹣3……(②)
第四步:2x﹣6x=24﹣3+1……(③)
第五步:﹣4x=22(④)
第六步:x=﹣![]() ……(⑤)
……(⑤)
以上解方程第二步到第六步的计算依据有:①去括号法则.②等式性质一.③等式性质二.④合并同类项法则.请选择排序完全正确的一个选项( )
A. ②①③④② B. ②①③④③ C. ③①②④③ D. ③①④②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直角坐标系xOy中,A(0,5),直线x=﹣5与x轴交于点D,直线y=﹣ ![]() x﹣
x﹣ ![]() 与x轴及直线x=﹣5分别交于点C,E,点B,E关于x轴对称,连接AB.
与x轴及直线x=﹣5分别交于点C,E,点B,E关于x轴对称,连接AB.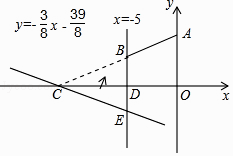
(1)求点C,E的坐标及直线AB的解析式;
(2)设面积的和S=S△CDE+S四边形ABDO , 求S的值;
(3)在求(2)中S时,嘉琪有个想法:“将△CDE沿x轴翻折到△CDB的位置,而△CDB与四边形ABDO拼接后可看成△AOC,这样求S便转化为直接求△AOC的面积不更快捷吗?”但大家经反复演算,发现S△AOC≠S,请通过计算解释他的想法错在哪里.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示为2013年7月份的日历示意图.
(1)请你计算虚线方框圈出的2×2个数(2行2列的4个数)的和;
(2)若方框圈出的2×2个数从左下角到右上角的2个数之和为46,则这4个数的最后一天是7月 日.(直接填空)
(3)若方框圈出的2×2个数的和最大,请你用方框将这4个数圈出来,并计算这4个数的和.
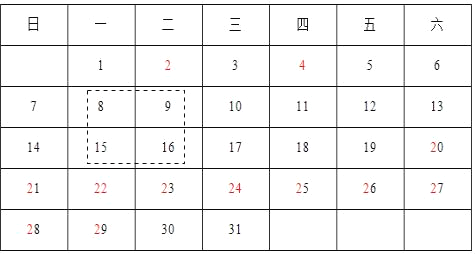
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com