
【题目】如图,在平行四边形ABCD中,![]() ,
,![]() 的平分线与BC的延长线交于点E,与DC交于点F,且点F为边DC的中点,
的平分线与BC的延长线交于点E,与DC交于点F,且点F为边DC的中点,![]() ,垂足为G,若
,垂足为G,若![]() ,则AE的边长为
,则AE的边长为![]()
![]()

A. ![]() B.
B. ![]() C. 4 D. 8
C. 4 D. 8
【答案】B
【解析】
试题由AE为角平分线,得到一对角相等,再由ABCD为平行四边形,得到AD与BE平行,利用两直线平行内错角相等得到一对角相等,等量代换及等角对等边得到AD=DF,由F为DC中点,AB=CD,求出AD与DF的长,得出三角形ADF为等腰三角形,根据三线合一得到G为AF中点,在直角三角形ADG中,由AD与DG的长,利用勾股定理求出AG的长,进而求出AF的长,再由三角形ADF与三角形ECF全等,得出AF=EF,即可求出AE的长.∵AE为∠DAB的平分线,∴∠DAE=∠BAE,∵DC∥AB,∴∠BAE=∠DFA,∴∠DAE=∠DFA,∴AD=FD,又F为DC的中点,∴DF=CF,∴AD=DF=![]() DC=
DC=![]() AB=2,在Rt△ADG中,根据勾股定理得:AG=
AB=2,在Rt△ADG中,根据勾股定理得:AG=![]() ,则AF=2AG=2
,则AF=2AG=2![]() ,∵平行四边形ABCD,∴AD∥BC,∴∠DAF=∠E,∠ADF=∠ECF,在△ADF和△ECF中,
,∵平行四边形ABCD,∴AD∥BC,∴∠DAF=∠E,∠ADF=∠ECF,在△ADF和△ECF中,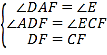 ,∴△ADF≌△ECF(AAS),∴AF=EF,则AE=2AF=4
,∴△ADF≌△ECF(AAS),∴AF=EF,则AE=2AF=4![]() .故选:B.
.故选:B.


 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案科目:初中数学 来源: 题型:
【题目】A、B两地果园分别有橘子40吨和60吨,C、D两地分别需要橘子30吨和70吨;已知从A、B到C、D的运价如表:
到C地 | 到D地 | |
A果园 | 每吨15元 | 每吨12元 |
B果园 | 每吨10元 | 每吨9元 |
(1)若从A果园运到C地的橘子为x吨,则从A果园运到D地的橘子为 ____吨,
从A果园将橘子运往D地的运输费用为 ____ 元.
(2)用含x的式子表示出总运输费(要求:列式、化简).
(3)求总运输费用的最大值和最小值.
(4)若这批橘子在C地和D地进行再加工,经测算,全部橘子加工完毕后总成本为w元,且w=-(x-25)2+4360.则当x= ___ 时,w有最 __ 值(填“大”或“小”).这个值是 __ .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线的顶点为A(1,4),抛物线与y轴交于点B(0,3),与x轴交于C,D两点.点P是x轴上的一个动点.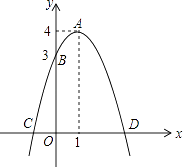
(1)求此抛物线的解析式;
(2)求C,D两点坐标及△BCD的面积;
(3)若点P在x轴上方的抛物线上,满足S△PCD= ![]() S△BCD , 求点P的坐标.
S△BCD , 求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正方形ABCD中,E是CD边上一点,
(1)将△ADE绕点A按顺时针方向旋转,使AD,AB重合,得到△ABF,如图1所示.观察可知:与DE相等的线段是 , ∠AFB=∠ 
(2)如图2,正方形ABCD中,P,Q分别是BC,CD边上的点,且∠PAQ=45°,试通过旋转的方式说明:DQ+BP=PQ 
(3)在(2)题中,连接BD分别交AP,AQ于M,N,你还能用旋转的思想说明BM2+DN2=MN2 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为2,E是CD的中点,将△ADE绕点A按顺时针方向旋转后得到△ABF,则EF的长等于( ) 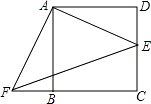
A.3
B.![]()
C.2 ![]()
D.3 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了鼓励居民节约用水,某市自来水公司对每户月用水量进行计费,每户每月用水量在规定吨数以下的收费标准相同;规定吨数以上的超过部分收费标准相同,以下是小明家![]() 月份用水量和交费情况:
月份用水量和交费情况:
月份 |
|
|
|
|
|
用水量(吨) |
|
|
|
|
|
费用(元) |
|
|
|
|
|
根据表格中提供的信息,回答以下问题:
![]() 求出规定吨数和两种收费标准;
求出规定吨数和两种收费标准;
![]() 若小明家
若小明家![]() 月份用水
月份用水![]() 吨,则应缴多少元?
吨,则应缴多少元?
![]() 若小明家
若小明家![]() 月份缴水费
月份缴水费![]() 元,则
元,则![]() 月份用水多少吨?
月份用水多少吨?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,BC是圆O的直径,点A,F在圆O上,连接AB,BF. 
(1)如图1,若点A、F把半圆三等分,连接OA,OA与BF交于点E.求证:E为OA的中点;
(2)如图2,若点A为弧 ![]() 的中点,过点A作AD⊥BC,垂足为点D,AD与BF交于点G.求证:AG=BG.
的中点,过点A作AD⊥BC,垂足为点D,AD与BF交于点G.求证:AG=BG.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,一次函数y=x+2的图象交y轴于点A,交x轴于点B,点E在x轴的正半轴上,OE=8,点F在射线BA上,过点F作x轴的垂线,点D为垂足,OD=6.
(1)写出点F的坐标 ;
(2)求证:∠ABO=45°;
(3)操作:将一块足够大的三角板的直角顶点放在线段BF的中点M处,一直角边过点E,交FD于点C,另一直角边与x轴相交于点N,如图2,求点N的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,下面不能判断是平行四边形的是( )

A. ∠B=∠D,∠A=∠C;
B. AB∥CD,AD∥BC
C. ∠B+∠DAB=180°,∠B+∠BCD=180°
D. AB∥CD,AB=CD
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com