
【题目】正方形ABCD中,E是CD边上一点,
(1)将△ADE绕点A按顺时针方向旋转,使AD,AB重合,得到△ABF,如图1所示.观察可知:与DE相等的线段是 , ∠AFB=∠ 
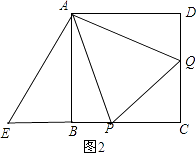
(2)如图2,正方形ABCD中,P,Q分别是BC,CD边上的点,且∠PAQ=45°,试通过旋转的方式说明:DQ+BP=PQ 
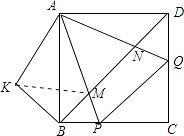
(3)在(2)题中,连接BD分别交AP,AQ于M,N,你还能用旋转的思想说明BM2+DN2=MN2 . 
【答案】
(1)BF;AED
(2)解:将△ADQ绕点A按顺时针方向旋转90°,则AD与AB重合,得到△ABE,如图2,
则∠D=∠ABE=90°,
即点E、B、P共线,∠EAQ=∠BAD=90°,AE=AQ,BE=DQ,
∵∠PAQ=45°,
∴∠PAE=45°,
∴∠PAQ=∠PAE,
在△APE和△APQ中
∵  ,
,
∴△APE≌△APQ(SAS),
∴PE=PQ,
而PE=PB+BE=PB+DQ,
∴DQ+BP=PQ
(3)解:∵四边形ABCD为正方形,
∴∠ABD=∠ADB=45°,
如图,将△ADN绕点A按顺时针方向旋转90°,则AD与AB重合,得到△ABK,
则∠ABK=∠ADN=45°,BK=DN,AK=AN,
与(2)一样可证明△AMN≌△AMK,得到MN=MK,
∵∠MBA+∠KBA=45°+45°=90°,
∴△BMK为直角三角形,
∴BK2+BM2=MK2,
∴BM2+DN2=MN2.
【解析】解:(1)∵△ADE绕点A按顺时针方向旋转,使AD、AB重合,得到△ABF,
∵DE=BF,∠AFB=∠AED.
故答案为:BF,AED;
(1)直接根据旋转的性质得到DE=BF,∠AFB=∠AED;(2)将△ADQ绕点A按顺时针方向旋转90°,则AD与AB重合,得到△ABE,根据旋转的性质得∠EAQ=∠BAD=90°,AE=AQ,BE=DQ,而∠PAQ=45°,则∠PAE=45°,再根据全等三角形的判定方法得到△APE≌△APQ,则PE=PQ,于是PE=PB+BE=PB+DQ,即可得到DQ+BP=PQ;(3)根据正方形的性质有∠ABD=∠ADB=45°,将△ADN绕点A按顺时针方向旋转90°,则AD与AB重合,得到△ABK,根据旋转的性质得∠ABK=∠ADN=45°,BK=DN,AK=AN,与(2)一样可证明△AMN≌△AMK得到MN=MK,由于∠MBA+∠KBA=45°+45°=90°,得到△BMK为直角三角形,根据勾股定理得BK2+BM2=MK2 , 然后利用等相等代换即可得到BM2+DN2=MN2 .


 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=8,BC=6.点E在边AB上,点F在边CD上,点G、H在对角线AC上.若四边形EGFH是菱形,则AE的长是( )

A. 2![]() B. 3
B. 3![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
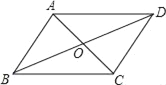
【题目】如图所示,在四边形ABCD中,对角线AC与BD相交于点O,AD∥BC,∠BAD=∠DCB,若不增加任何字母和辅助线,要使得四边形ABCD是矩形,则还需要增加一个条件是_______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在平面直角坐标系中有三点A(﹣2,1)、B(3,1)、C(2,3).请回答如下问题:
(1)在坐标系内描出点A、B、C的位置,并求△ABC的面积;
(2)在平面直角坐标系中画出△A′B′C′,使它与△ABC关于x轴对称,并写出△A′B′C′三顶点的坐标;
(3)若M(x,y)是△ABC内部任意一点,请直接写出这点在△A′B′C′内部的对应点M′的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中,正确的有( )
①射线![]() 和射线
和射线![]() 是同一条射线.②将一根细木条固定在墙上,至少需要钉两个钉子,其理论依据是:两点之间线段最短.③两点间的连线的长度叫做这两点间的距离.
是同一条射线.②将一根细木条固定在墙上,至少需要钉两个钉子,其理论依据是:两点之间线段最短.③两点间的连线的长度叫做这两点间的距离.
④表示北偏东![]() 方向、南偏东
方向、南偏东![]() 方向的两条射线所夹的角为直角.
方向的两条射线所夹的角为直角.
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,![]() ,
,![]() 的平分线与BC的延长线交于点E,与DC交于点F,且点F为边DC的中点,
的平分线与BC的延长线交于点E,与DC交于点F,且点F为边DC的中点,![]() ,垂足为G,若
,垂足为G,若![]() ,则AE的边长为
,则AE的边长为![]()
![]()

A. ![]() B.
B. ![]() C. 4 D. 8
C. 4 D. 8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知数轴上两点A、B所表示的数分别为a和b,且满足|a+3|+(b-9)2018=0,O为原点
(1) 试求a和b的值
(2) 点C从O点出发向右运动,经过3秒后点C到A点的距离是点C到B点距离的3倍,求点C的运动速度?
(3) 点D以1个单位每秒的速度从点O向右运动,同时点P从点A出发以5个单位每秒的速度向左运动,点Q从点B出发,以20个单位每秒的速度向右运动.在运动过程中,M、N分别为PD、OQ的中点,问![]() 的值是否发生变化,请说明理由.
的值是否发生变化,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在实施漓江补水工程中,某水库需要将一段护坡土坝进行改造.在施工质量相同的情况下,甲、乙两施工队给出的报价分别是:甲施工队先收启动资金1000元,以后每填土1立方米收费20元,乙施工队不收启动资金,但每填土1立方米收费25元.
(1)设整个工程需要填土为X立方米,选择甲施工队所收的费用为Y甲元,选择乙施工队所收的费用为Y乙元.请分别写出Y甲、Y乙、关于X的函数关系式;
(2)如图,土坝的横截面为梯形,现将背水坡坝底加宽2米,即BE=2米,已知原背水坡长AB=4![]() ,土坝与地面的倾角∠ABC=60度,要改造100米长的护坡土坝,选择哪家施工队所需费用较少?
,土坝与地面的倾角∠ABC=60度,要改造100米长的护坡土坝,选择哪家施工队所需费用较少?
(3)如果整个工程所需土方的总量X立方米的取值范围是100≤X≤800,应选择哪家施工队所需费用较少?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com