练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，矩形ABCD中，AB=8，BC=6．点E在边AB上，点F在边CD上，点G、H在对角线AC上．若四边形EGFH是菱形，则AE的长是（　　）

    A. 2 B. 3 C. D.

    【答案】D

    【解析】连接EF交AC于点M，由菱形的性质可得FM=EM，EF⊥AC；利用“AAS或ASA”易证△FMC≌△EMA，根据全等三角形的性质可得AM=MC；在Rt△ABC中，由勾股定理和解直角三角形的性质求解即可.

    如图，连接EF交AC于点M，由四边形EGFH为菱形可得FM=EM，EF⊥AC；利用“AAS或ASA”易证△FMC≌△EMA，根据全等三角形的性质可得AM=MC；在Rt△ABC中，由勾股定理求得AC=10，且tan∠BAC=；在Rt△AME中，AM=AC=5，tan∠BAC=，可得EM=；在Rt△AME中，由勾股定理求得AE==6.25．

    故选：B．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】我们规定：平面内点A到图形G上各个点的距离的最小值称为该点到这个图形的最小距离d，点A到图形G上各个点的距离的最大值称为该点到这个图形的最大距离D，定义点A到图形G的距离跨度为R=D﹣d．
    （1）①如图1，在平面直角坐标系xOy中，图形G1为以O为圆心，2为半径的圆，直接写出以下各点到图形G1的距离跨度：
    A（﹣1，0）的距离跨度；
    B（ ，﹣ ）的距离跨度；
    C（﹣3，2）的距离跨度；
    ②根据①中的结果，猜想到图形G1的距离跨度为2的所有的点组成的图形的形状是 ．

    （2）如图2，在平面直角坐标系xOy中，图形G2为以C（1，0）为圆心，2为半径的圆，直线y=k（x+1）上存在到G2的距离跨度为2的点，求k的取值范围．

    （3）如图3，在平面直角坐标系xOy中，射线OA：y= x（x≥0），圆C是以3为半径的圆，且圆心C在x轴上运动，若射线OA上存在点到圆C的距离跨度为2，直接写出圆心C的横坐标xc的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】二次函数y=ax2+bx+c的图象如图，点（1，0）在函数图象上，那么abc、2a+b、a+b+c、a﹣b+c这四个代数式中，值大于或等于零的数有（ ）
    A.1个
    B.2个
    C.3个
    D.4个

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知：∠B=∠DEF，AB=DE，要说明△ABC≌△DEF.（1）若以“ASA”为依据，还缺条件 _________________ ；（2）若以“AAS”为依据，还缺条件___________________；（3）若以“SAS”为依据，还缺条件___________________；

    查看答案和解析>>

    科目：初中数学 来源： 题型：

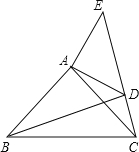
    【题目】已知：如图，在△ABC、△ADE中，∠BAC=∠DAE=90°，AB=AC，AD=AE，点C、D、E三点在同一直线上，连接BD．

    （1）求证：△BAD≌△CAE；

    （2）试猜想BD、CE有何特殊位置关系，并证明．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】正方形ABCD中，F是AB上一点，H是BC延长线上一点，连接FH，将△FBH沿FH翻折，使点B的对应点E落在AD上，EH与CD交于点G，连接BG交FH于点M，当GB平分∠CGE时，BM=2，AE=8，则ED=______．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】A、B两地果园分别有橘子40吨和60吨，C、D两地分别需要橘子30吨和70吨；已知从A、B到C、D的运价如表：

    到C地

    到D地

    A果园

    每吨15元

    每吨12元

    B果园

    每吨10元

    每吨9元

    （1）若从A果园运到C地的橘子为x吨，则从A果园运到D地的橘子为 ____吨，

    从A果园将橘子运往D地的运输费用为 ____ 元．

    （2）用含x的式子表示出总运输费（要求：列式、化简）．

    （3）求总运输费用的最大值和最小值．

    （4）若这批橘子在C地和D地进行再加工，经测算，全部橘子加工完毕后总成本为w元，且w＝－(x－25)2＋4360．则当x＝ ___ 时，w有最 __ 值（填“大”或“小”）．这个值是 __ ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某商店三、四月份出售同一品牌各种规格空调销售台输入下表，回答：

    匹

    匹

    匹

    匹

    三月

    四月

    商店平均每月销售空调________台；

    商店出售各种规格的空调中，众数有________匹；

    在研究六月份进货时，商店经理决定________（匹）的空调要多进，________（匹）的空调要少进．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】正方形ABCD中，E是CD边上一点，
    （1）将△ADE绕点A按顺时针方向旋转，使AD，AB重合，得到△ABF，如图1所示．观察可知：与DE相等的线段是 ， ∠AFB=∠

    （2）如图2，正方形ABCD中，P，Q分别是BC，CD边上的点，且∠PAQ=45°，试通过旋转的方式说明：DQ+BP=PQ

    （3）在（2）题中，连接BD分别交AP，AQ于M，N，你还能用旋转的思想说明BM2+DN2=MN2 ．

    查看答案和解析>>

    同步练习册答案