
【题目】如图,已知:∠B=∠DEF,AB=DE,要说明△ABC≌△DEF.(1)若以“ASA”为依据,还缺条件 _________________ ;(2)若以“AAS”为依据,还缺条件___________________;(3)若以“SAS”为依据,还缺条件___________________;

【答案】 ∠A=∠D ∠ACB=∠F BC=EF;
【解析】(1)根据题目所给条件和判定三角形全等的条件可得添加条件:∠A=∠D;
(2)根据题目所给条件和判定三角形全等的条件可得添加条件:∠ACB=∠F;
(3)根据题目所给条件和判定三角形全等的条件可得添加条件:CB=EF.
(1)添加条件:∠A=∠D,
∵在△ABC和△DEF中,
∵∠A=∠D,
AB=DE,
∠B=∠DEF,
∴△ABC≌△DEF(ASA),
故答案为:∠A=∠D.
(2)添加条件:∠ACB=∠F,
在△ABC和△DEF中,
∵∠ACB=∠F,
∠B=∠DEF,
AB=DE,
∴△ABC≌△DEF(AAS),
故答案为:∠ACB=∠F.
(3)添加条件:CB=EF,
在△ABC和△DEF中,
∵AB=DE,
∠B=∠DEF,
BC=EF,
∴△ABC≌△DEF(SAS),
故答案为:CB=FE.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】为应对越来越严重的雾霾天气,孔明同学所在班级的家长委员会,准备为该班集资捐赠一台大型的空气净化机,现知道某商场将该型号的空气净化机按标价的八折出售,每台空气净化机仍可获利![]() ,已知该型号客气净化机的进价为
,已知该型号客气净化机的进价为![]() 元.
元.
![]() 求该空气净化机的标价.
求该空气净化机的标价.
![]() 若该班有
若该班有![]() 名学生,则该班每位学生家长应平均捐助多少元.
名学生,则该班每位学生家长应平均捐助多少元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
如图1,在平面直角坐标系xOy中,直线y1=ax+b与双曲线y2= ![]() 交于A(1,3)和B(﹣3,﹣1)两点.
交于A(1,3)和B(﹣3,﹣1)两点.
观察图象可知:
①当x=﹣3或1时,y1=y2;
②当﹣3<x<0或x>1时,y1>y2 , 即通过观察函数的图象,可以得到不等式ax+b> ![]() 的解集.
的解集.
有这样一个问题:求不等式x3+4x2﹣x﹣4>0的解集.
某同学根据学习以上知识的经验,对求不等式x3+4x2﹣x﹣4>0的解集进行了探究.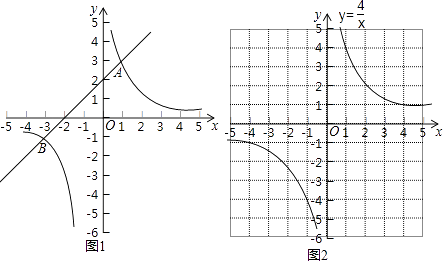
下面是他的探究过程,请将(2)、(3)、(4)补充完整:
(1)将不等式按条件进行转化:
(2)构造函数,画出图象
设y3=x2+4x﹣1,y4= ![]() ,在同一坐标系中分别画出这两个函数的图象.
,在同一坐标系中分别画出这两个函数的图象.
双曲线y4= ![]() 如图2所示,请在此坐标系中画出抛物线y3=x2+4x﹣1;(不用列表)
如图2所示,请在此坐标系中画出抛物线y3=x2+4x﹣1;(不用列表)
(3)确定两个函数图象公共点的横坐标,观察所画两个函数的图象,猜想并通过代入函数解析式验证可知:满足y3=y4的所有x的值为
(4)借助图象,写出解集
结合(1)的讨论结果,观察两个函数的图象可知:不等式x3+4x2﹣x﹣4>0的解集
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD内接于⊙O,点E在对角线AC上,EC=BC=DC. 
(1)若∠CBD=39°,求∠BAD的度数;
(2)求证:∠1=∠2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2016.镇江)如图,AD、BC相交于点O,AD=BC,∠C=∠D=90°.
(1)若∠ABC=35°,求∠CAO的度数;
(2)求证:CO=DO

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=8,BC=6.点E在边AB上,点F在边CD上,点G、H在对角线AC上.若四边形EGFH是菱形,则AE的长是( )

A. 2![]() B. 3
B. 3![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
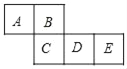
【题目】如图是一个无盖正方体纸盒的表面展开图,请解答下列问题:
(1)若在图上补上一个同样大小的正方形F,便它能围成一个正方体,共有 种补法;
(2)请画出两种不同的补法;
(3)设A=a3+a2b+3,B=a2b﹣3,C=a3﹣1,D=6﹣a2b,若(2)中的展开图围成正方体后.相对两个面的代数式之和都相等,分别求E、F所代表的代数式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com